Foams and Honeycombs
By Erica Klarreich
For centuries, the precise architecture of soap foams has been a source of wonder to children and a challenge to mathematicians
For centuries, the precise architecture of soap foams has been a source of wonder to children and a challenge to mathematicians

DOI: 10.1511/2000.19.152
Nearly all of us have been enchanted at some time in our lives by the fragile symmetry of soap bubbles and soap films. But few have had the privilege of being introduced to them by a great scientist, as Agnes Gardner King did.
In the fall of 1887, the fledgling painter paid a visit to her uncle, Lord Kelvin (then Sir William Thomson), a physicist who was already renowned for his work in thermodynamics. A day after arriving, she recorded that:
Uncle William and Aunt Fanny met me at the door, Uncle William armed with a vessel of soap and glycerine prepared for blowing soap bubbles, and a tray with a number of mathematical figures made of wire. These he dips into the soap mixture and a film forms and adheres to the wires very beautifully and perfectly regularly. With some scientific end in view he is studying these films.
Kelvin was drawn to soap films in the course of his efforts to understand the nature of light. By the late 19th century, a multitude of experiments had shown that light exhibits wavelike properties, and many scientists sought to explain light by describing some sort of medium, called the "ether," through which light waves would propagate. Kelvin conceived of a foamlike model for the ether, so he attacked the problem of understanding what would be the structure of the most perfect possible foam, one in which all the bubbles have the same volume. Kelvin realized that this question could be boiled down to the following purely mathematical problem: What is the best way to divide three-dimensional space into cells of equal volume, if one wants to minimize the surface area of the cell walls?

Image by John M. Sullivan, University of Illinois
Over the course of two months, Kelvin searched for the shape that would form the best partition. By November 4, 1887, he had found what he believed to be the answer, a polyhedron to which he gave the tongue-twisting name of "tetrakaidecahedron" (meaning 14-sided polyhedron) but which is more commonly known as the truncated octahedron. Copies of this shape, placed next to each other, fill all of space, with a lower surface area than more familiar partitions, such as a partition into cubical "rooms." Kelvin's partition is highly symmetrical, like the cubical partition, and has a strong aesthetic appeal.
Although Kelvin did not prove that the truncated octahedron was the best possible division of space, for more than a century his solution was generally accepted as correct. It received the stamp of approval from such illustrious mathematicians as Hermann Weyl, who wrote of it in 1952 in his famous book, Symmetry. But in 1994, physicists Denis Weaire of Trinity College Dublin and Robert Phelan, now at the Shell Research and Technology Center in Amsterdam, astonished mathematicians and physicists by producing a partition of space with lower surface area. Weaire and Phelan's partition, like Kelvin's, was inspired by naturally occurring structures, this time from chemistry.
One of the reasons that scientists expected Kelvin's solution to hold up was that his partition is one of the most appealing, most symmetrical divisions of space. It is an intriguing phenomenon in the sciences that aesthetically pleasing solutions seem to have a higher chance of being correct than more complicated, less symmetric ones (a topic elaborated in these pages by James W. McAllister in March–April 1998). As Oxford University mathematician and physicist Roger Penrose put it,
I have noticed on many occasions in my own work where there might, for example, be two guesses that could be made as to the solution of a problem and in the first case I would think how nice it would be if it were true; whereas in the second case I would not care very much about the result even if it were true. So often, in fact, it turns out that the more attractive possibility is the true one—or that while thinking about the problem in this way the true solution would finally emerge to reveal itself as even more attractive than either contemplated earlier.
Weaire and Phelan's structure, which is less symmetrical than Kelvin's, is a reminder that our inclination toward beautiful solutions must always be examined critically—especially when nature itself provides an alternative. On the other hand, in the past two years Thomas Hales, a colleague of mine at the University of Michigan, has struck a blow for symmetry in two other problems related to foams: the Kepler conjecture, which states that the way to pack equal-volume balls together with the least wasted space is the familiar pyramid packing used to stack fruit in groceries (discussed in Science Observer, November–December 1998); and the honeycomb problem, a two-dimensional version of the Kelvin question. The study of foams, then, seems to be a subject poised very delicately between complexity and symmetry, and one in which the final word has not yet been said.
Kelvin opened his article on partitioning space with the words, "this problem is solved in foam." It may not be obvious that mathematics applies to foams, but indeed physics and mathematics are intimately intertwined in soap films.
The force that enables soap bubbles to exist is known as surface tension and is caused by the attraction between the molecules of a soap film. Since the molecules tend to pull together, maintaining a large surface area is energy-expensive; the soap film naturally deforms toward the surface of least area and lowest energy.
Photograph by Mike Jewkes, Hunterian Museum, University of Glasgow; illustration adapted from Surface Evolver image generated by Kenneth Brakke, Susquehanna University.
Consider what happens when you dip a circular wire into a soapy liquid. When you draw it out, you see a beautiful iridescent soap film shaped like a flat disk. In this simple case, it is possible to confirm mathematically that the flat disk is the lowest-area surface that the wire can support. What if I dip a more complicated wire loop into the soap solution? The surface that forms when I draw out the wire is no longer as familiar, but there are still some things that mathematicians can say about it. When a wire loop supports a soap film, the air pressures on both sides of the film are equal. Setting aside gravity, which is much weaker than surface tension for a small soap film, the only forces that can disturb the balance of the film are the attractive forces of the film's own molecules.
Therefore, in order for the soap film to be in equilibrium, the attractive forces that the molecules exert on one another must exactly cancel one another. This happens, for example, at the central point (or "saddle point") of a saddle surface. On the saddle, many of the molecules lie higher up than the saddle point; these molecules exert an upward pull on the saddle point. On the other hand, just as many molecules lie lower than the saddle point, so the upward and downward forces balance each other, leaving the saddle point in equilibrium. When the attractive forces cancel one another at every point, the film is called a surface of zero mean curvature. Such films are the only ones that can form on a wire frame.
The most familiar soap film of all is, of course, the round soap bubble. Unlike the soap films that exist on wire loops, the soap bubble does not have zero mean curvature. If you look at a molecule at the "north pole" of a bubble, you see that all of the nearby molecules are lower, so there is a net downward force on that molecule, toward the center of the bubble. Likewise, surface tension causes an inward force at every other point on the sphere. Mathematicians say that the sphere has positive mean curvature.
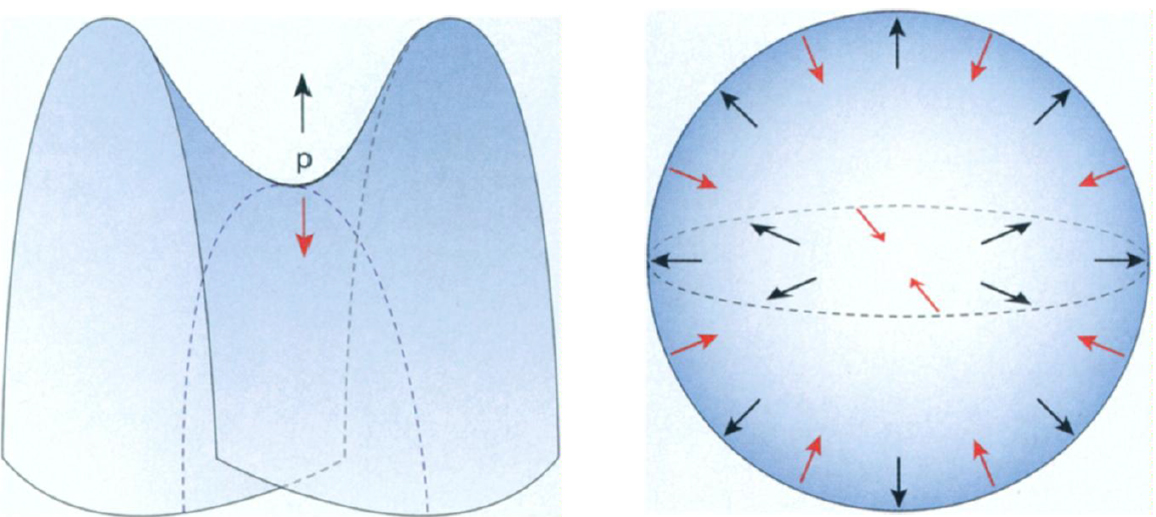
Why, then, don't soap bubbles implode? Since the bubbles have no wire loops to support them, surface tension seems to dictate that they should collapse in on themselves. But we all have seen spherical soap bubbles floating freely through the air, oblivious to the forces that seem to call for their destruction. The answer to this apparent contradiction lies in the pressure difference inside and outside the bubble. As a soap bubble starts to contract, the air inside the bubble exerts a greater pressure than the air on the outside, so that the inside air pushes outward on the soap bubble. The bubble finds its equilibrium in the sphere whose inward surface tension exactly balances this outward push.
The mathematician Pappus of Alexandria wrote the first careful mathematical analysis of the spherical shape of soap bubbles in 320 a.d., although it is likely that the ideas he described originated as much as 500 years earlier with the Greek mathematician Zenodorus. The first rigorous proof, using calculus, that the sphere has the least area of any figure containing a given volume was not given until 1884 by the German mathematician H. A. Schwarz. A somewhat easier version of the problem, called the "isoperimetric problem," is to show that a circle has the least perimeter of any plane figure enclosing a given area. This can be proved without calculus, and indeed Pappus gave such a proof.
Soap-bubble problems remain notoriously hard to solve mathematically. Take, for example, the "double bubble" theorem, which says that the best way to enclose two equal volumes is within two spherical pieces that meet along a common flat wall, forming a double bubble. In spite of the fact that this seems like the obvious choice, the double-bubble problem is so hard that it only yielded to rigorous mathematical proof as recently as 1995, by the mathematicians Joel Hass and Roger Schlafly of the Davis and Santa Cruz campuses, respectively, of the University of California. (See "Bubbles and Double Bubbles," September–October 1996).
The Kelvin problem is about dry foams, foams in which there is so little liquid that the walls may be regarded as having negligible thickness. Recently, significant progress has been made in understanding wet foams, in which there is a substantial liquid content acting as a cushion between the bubbles. How will equal-volume bubbles arrange themselves in a wet foam? This question, a not-too-distant cousin of Kelvin's problem, leads to another centuries-old problem that was solved by Hales in August 1998.
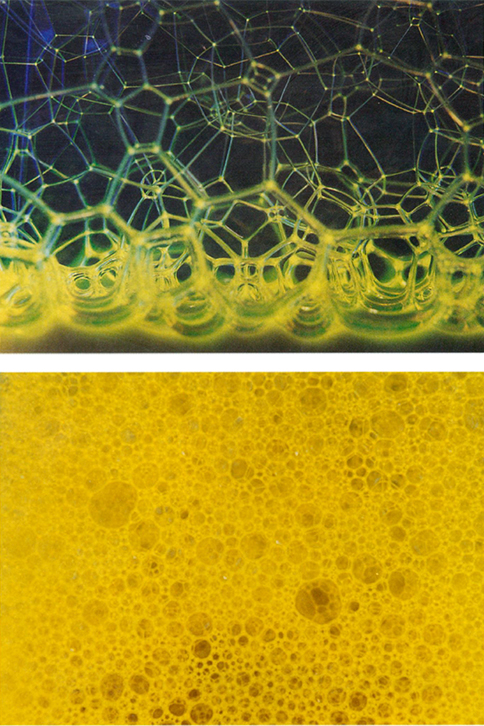
Photographs courtesy of Burkhard Prause, University of Notre Dame
When a foam has a high liquid content, the individual bubbles have much more freedom of shape than in a dry foam, because they do not directly touch each other. If there is enough liquid, each bubble will independently minimize its surface area, taking (as Schwarz proved) the shape of a sphere. So the question becomes, what is the way to pack equal-volume spheres together with the least wasted space? At the beginning of the 17th century the great physicist Johannes Kepler proposed an answer: The best way should be the most natural one, namely, the pyramid stacking. This hypothesis became known as the Kepler conjecture, and in spite of many efforts it resisted proof until just a year and a half ago.

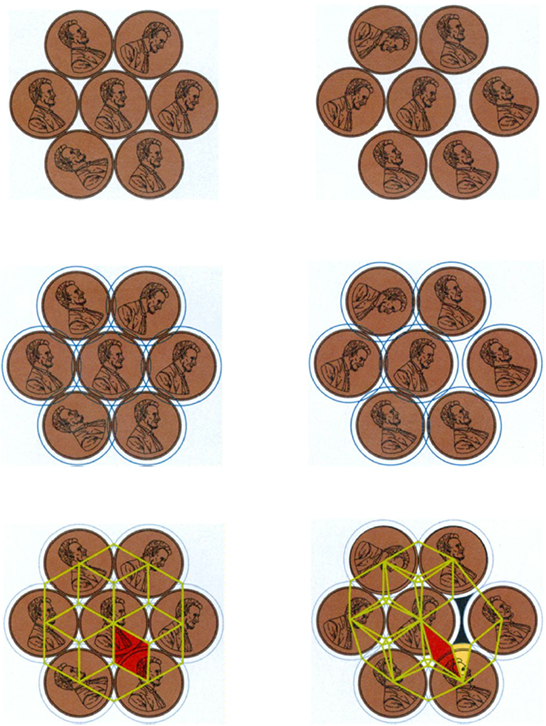
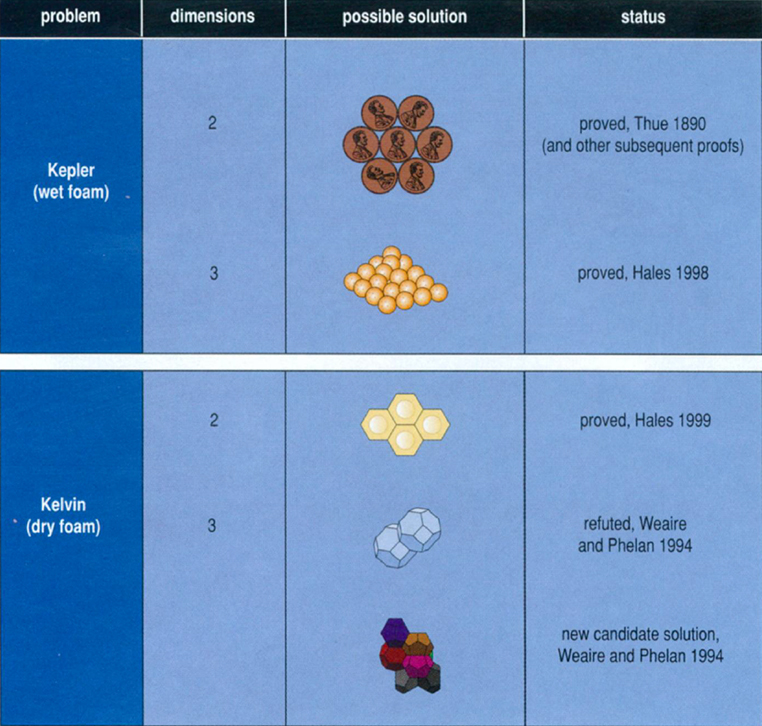
Hales's approach to the Kepler conjecture can be understood by an analogy with the two-dimensional version of the problem. Instead of packing together spheres in space, suppose I try to cover a flat surface with closely packed circular objects, such as pennies. Imagine trying to lay down the pennies on an infinitely large table, in such a way that they never overlap. What is the way to do this with the least wasted space? Since the table and the collection of pennies are infinite, strictly speaking I am trying to minimize the amount of wasted space per penny. One natural way to arrange pennies is simply to line them up in horizontal rows and then place the rows next to each other so that the pennies line up vertically as well as horizontally; then the pennies lie inside squares. Another way is to line the pennies up in rows, but then place each row into the indentations of the row beneath it; now the pennies lie inside hexagons. Common sense tells me that the hexagon arrangement wastes less space than the square arrangement. The hexagon pattern is, in fact, the best possible packing of pennies; this can be proved using elementary mathematics. A key step is to cut a penny pattern up into three different types of small, easily-handled pieces (see Figure 6, below), and then to compute the percentage of wasted space on each of these pieces.
Carving space into small pieces is also essential to Hales's proof of the three-dimensional Kepler conjecture, since it transforms an infinite problem into a finite, although huge, problem. His decomposition produces about 5,000 different cases to consider. Hales employed the calculating power of computers to knock these cases down one by one. His final proof, excluding computer work, requires several hundred pages. The monumental effort that went into this proof stands in sharp contrast to the simplicity of the statement of the Kepler conjecture. It hints at the challenges that may lie in the way of answering the still more difficult Kelvin question, in which instead of packing together identical spheres we must consider infinitely many different possible cell shapes.
What if I try moving down to two dimensions to consider the Kelvin problem? Now my cells will be two-dimensional, and the walls between cells will be lines (or maybe curves). Now, what is the partition of the plane into equal-area cells that minimizes the total length of the walls? If I restrict my attention to partitions in which all the cells are identical regular polygons, only three patterns or "tessellations" emerge: tilings of the plane by squares, by equilateral triangles and by hexagons. It is not hard to show that the best of these three is the hexagonal pattern, which I recognize from the honeycomb of bees and also from the two-dimensional Kepler problem. Intuition suggests that this should remain the best partition, even when I widen my scope to allow nonidentical or irregular polygons. Astonishingly, the conjecture that the honeycomb pattern is the best, which dates back thousands of years, was only proved last year, by Hales.
Hales was led to the honeycomb problem in the wake of the excitement caused by his proof of the Kepler conjecture. His announcement that he had completed a proof catapulted him instantly into the limelight, and in March of 1999 he was asked to present a public lecture on his work at the University of Michigan. Hales decided to conclude the talk by describing some open problems related to Kepler's conjecture, giving each one a difficulty rating. To his mind, the Kelvin question was clearly a 10-star problem. But he could not decide how many stars to give the honeycomb problem. "The honeycomb question had been around for more than 2,000 years, but I felt certain that it was easier than the Kelvin question," he said. "Finally I decided, if it was so simple, that I should sit down and try to solve it."
For Hales, the Kepler conjecture, the honeycomb problem and the Kelvin question all have the same attraction. "It's easy to be trapped by these problems," he said. "They sound so simple, you think they can't be that hard. By the time you realize that you're wrong, you are in too deep to stop." Luckily for Hales, his intuition that the honeycomb problem was approachable did not play him false. With the expertise that he had built up in his years of work on the Kepler conjecture, it was only six months before he was able to announce a proof of the honeycomb problem. Unlike his proof of the Kepler conjecture, this new proof makes no use of computers and is only 20 pages long; comparatively speaking, it fell into his lap. Hales wrote, "in contrast with the years of forced labor that gave the proof of the Kepler conjecture, I felt as if I had won the lottery."

Photograph by Jeff Pettis, courtesy of the Agricultural Research Service, U.S. Department of Agriculture.
Hales's proof hinged on finding a new isoperimetric inequality, relating the perimeter and the area of a figure, that was optimized by the hexagonal pattern. As noted above, the best way to enclose a single region is within a circle; however, circles do not fill a plane without leaving gaps. The problem for Hales, then, was to find some appropriate way to "penalize" the circle for its roundness. This turned out to be a delicate balancing act. "It was easy to go overboard," Hales said, "and come up with an inequality that carved too much out of the circle." Once he had fine-tuned the area-perimeter restriction, Hales was able to build upon work in geometric measure theory, a branch of mathematics that has developed over the course of this century, to prove that the honeycomb pattern is indeed the best way to tile the plane.
The appearance of the hexagonal pattern in the honeycomb of bees gives rise to an interesting philosophical question: Are bees mathematicians? The symmetry of the bees' honeycomb has fascinated beholders throughout history; in the Arabian Nights, the bee says, "My house is constructed according to the laws of a most severe architecture; and Euclid himself could learn from studying the geometry of my cells." The hexagon pattern is certainly advantageous for the bees, since little wax is needed to build the walls; but how do the bees know that this is so? It is hard to imagine that they perform the complicated mathematical analysis that shows that the hexagon pattern is the best arrangement. One explanation, popular in the 18th century, was that bees followed "divine" intuition when making their cells. With the advent of Darwinism in the second half of the 19th century, it became fashionable to attribute it to natural selection. Darwin himself wrote, "Beyond this stage of perfection in architecture natural selection [which now has replaced divine guidance!] could not lead; for the comb of the hive-bee, as far as we can see, is absolutely perfect in economizing labor and wax." Still others have suggested that the hexagonal design arises not through any intention or instinct of the bees but because the cells of the honeycomb are formed when heated wax forms bubbles, and these bubbles should obey the same area-minimizing principles as soap bubbles.
Curiously, a three-dimensional honeycomb partition is not optimal. A honeycomb cell is a hexagonal prism capped off on one end by three rhombi (Figure 8). The full honeycomb consists of two layers of these cells, stacked together so that the caps of one layer fit into the gaps of the other, like a jigsaw puzzle. For many years it was believed that this was the best two-layer arrangement, but in 1964 the Hungarian mathematician L. Fejes Tóth showed that a hexagonal cell capped off by part of a truncated octahedron would produce a tiny saving. Tóth pointed out, however, that the bees could have excellent reasons for choosing a slightly less efficient structure. Because the honeycomb walls have a definite thickness, it is not clear that Tóth's structure would indeed be an improvement. In that respect, the honeycomb is more like a wet foam than a dry foam. Recently, Weaire and Phelan undertook to construct two-layer foams with equal-sized bubbles, and they found that the dry foams did take on Tóth's pattern. But when they gradually added liquid, they wrote, something "quite dramatic" happened: The structure suddenly switched over to the bees' configuration. It seems, then, that the bees got it right after all.
If the two-layer honeycomb problem, which deals with partitioning part of space into cells, is so difficult, then the Kelvin question, about partitioning all of space, is infinitely more so. It might seem that every configuration of cells that fills up space is a potential candidate for the answer to the Kelvin question; in that case it would be necessary to check through the entire multitude of cell arrangements. However, at the end of the 19th century, the Belgian physicist Joseph Plateau evolved some basic principles that guide the search for viable partitions. Although the soap films that appear in nature seem completely random, Plateau made the surprising observation that the walls of a soap film can meet in only two ways. When they meet at a junction, it is always in threes, and at angles of 120 degrees, as in Figure 9a (below). What's more, the corners of the "rooms" of a soap film can only meet each other in groups of four, with corner angles of about 109 degrees, as at the point at the center of the tetrahedral pattern of Figure 9b. Plateau himself was struck with the simplicity of his rules, writing, "... these laws lead us to a very remarkable consequence: the froth which forms on certain liquids, for example on champagne, beer or agitated soap water, is evidently an assemblage of liquid films.... Consequently, though everything in the froth seems ruled by chance, it must be subject to those same laws." Nature does not give us a choice.

Photographs courtesy of Michele Emmer, University of Rome "La Sapienza."
Although Plateau's principles seem unexpected at first, they are rooted in questions of stability. Imagine that I have a foam in which four walls meet at a junction, instead of three; for simplicity I will assume that they meet at right angles, so that a small portion of the foam looks like the shape in Figure 9c. By comparison, the foam of Figure 9d, in which the fourfold junction has split apart into two threefold junctions, has lower area. The four-wall junction will therefore be unstable and will quickly deform into a foam with two threefold junctions. Similar considerations explain Plateau's other principle, although a fully rigorous mathematical proof of them was not given until 1976 by the Rutgers University mathematician Jean Taylor.
Even with Plateau's principles in mind, it is not an easy task to decide whether a given shape or collection of shapes can fill space without any gaps or overlap, as Kelvin's question requires. But it is easy to produce a wealth of shapes that do fill space, by building what are known as Voronoi cells. To construct Voronoi cells I must start with an infinite collection of tiny bubbles located at different points in space, then let the bubbles expand until they bump into each other. If the centers of the bubbles are chosen with a little care, the cells produced in this way will be finite polyhedra that fill all of space; if the centers are chosen to form a repeating pattern, the Voronoi cells will also form a repeating pattern. I can do the same thing in two dimensions. (See Figure 10, below.)
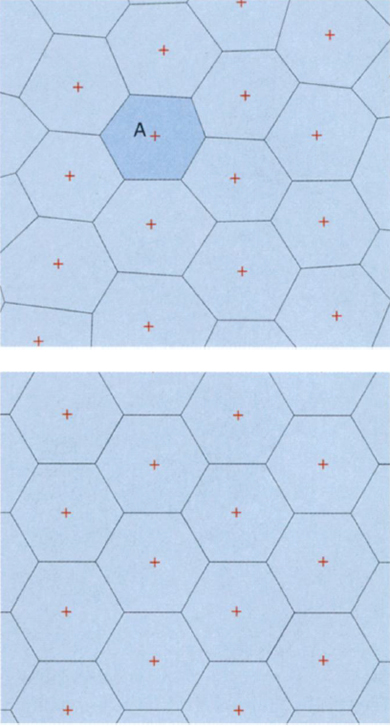
In the plane, the Voronoi-cell construction sets up a tight correspondence between the Kepler and Kelvin problems. If I place my "bubbles" at the centers of the pennies in the best penny packing and expand them into Voronoi cells, I get a honeycomb, which is the solution to the Kelvin question. So in the search for the solution to the three-dimensional Kelvin question, it makes sense to start with the Voronoi cells that correspond to the best sphere packing, Kepler's pyramid arrangement. If I allow the spheres of the pyramid packing to swell until they bump into their neighbors, I get 12-sided figures called rhombic dodecahedra. These form a partition of space with very low surface area, but it is not quite as low as that of a few other configurations, including Kelvin's truncated octahedra. On the other hand, if I construct Voronoi cells by placing my bubbles not at the centers of the spheres but instead as far away from the spheres as possible, I get truncated octahedra. Thus, in both two and three dimensions, the Kepler packing produces excellent candidates for the answer to the Kelvin question.
The parallel between the two- and three-dimensional cases only goes so far, however. In dimension 2, Hales proved last year that the hexagon pattern is the best partition of the plane. In dimension 3, the truncated octahedra themselves are not even a reasonable candidate for the best decomposition of space, for they do not obey Plateau's requirements. Truncated octahedra are 14-sided polyhedra consisting of six squares and eight hexagons, so the angles they form at corners are 90 and 120 degrees, not the 109-degree angles that appear in a foam. Kelvin realized this, and to correct the angles he distorted the figure slightly, being careful to keep the mean curvature equal to zero; thus Kelvin's final figure has slightly curved faces. Kelvin wrote that "no shading could show satisfactorily the delicate curvature of the hexagonal faces," but he pointed out that the shape can be made perfectly by dipping a certain wire structure into a soap solution and removing it. In fact he did construct a wire model of his partition that has subsequently been called "Kelvin's Bedspring."
For over a century, Kelvin's solution was the undisputed champion; all that was missing was a proof. The proof did not materialize, however, and in 1994 Weaire and Phelan finally explained why: Kelvin's partition is not the best way to fill space.
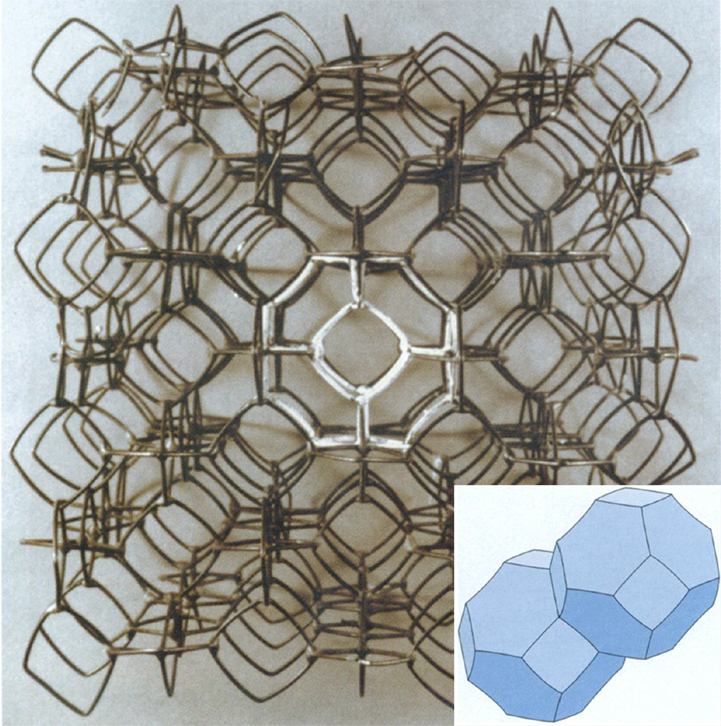
When Weaire and Phelan started looking for good models for foam structures, yet another branch of science came into play: chemistry. Weaire and Phelan found inspiration in a class of compounds called clathrates, chemicals in which certain atoms are enclosed within the crystals of other atoms. An especially promising structure was the compound Na8Si46, in which the eight atoms of sodium (Na) are contained in "cages" whose corners are the silicon (Si) atoms. These cages are exactly the Voronoi cells of the sodium atoms. This crystalline structure is a good foam candidate because the cages obey Plateau's principles, with walls that meet at threefold junctions and corners that meet in groups of four (although like Kelvin's structure, the walls must be slightly curved to have the correct angles). What's more, experimental evidence suggests that configurations with low surface area tend to have many 14-sided polyhedra; the Na8Si46 molecule consists of eight cages, six of which are identical 14-sided cells (the other two cells are 12-sided). Using this molecule as their model, Weaire and Phelan designed a partition of space into eight-room blocks. This is more complicated than Kelvin's partition, in which space is filled by copies of a single truncated octahedron room.

Images a and b courtesy of Kenneth Brakke, Susquehanna University; large image courtesy of Stuart Levy and John Sullivan, University of Illinois.
Once Weaire and Phelan had constructed their partition, they turned to a tool that was certainly not available to Kelvin: a computer program called the Surface Evolver, designed by Kenneth Brakke of Susquehanna University, which they used to adjust the curvature of the walls so that their surface area would be as small as possible. Interestingly, Weaire and Phelan began their investigation of this structure in an attempt to approach physical questions of wet foams, and not to try to surpass Kelvin's truncated octahedron. They ended with what Weaire called a "startling result": a structure that outdid Kelvin's!
Weaire and Phelan's successful rival to Kelvin's structure is not necessarily the end of the story. There are many other clathrate chemicals that might give rise to interesting divisions of space, and there is even the possibility that the best way to partition space into cells of equal volume is not a repeating pattern at all but a completely random decomposition. "I suspect that it will be 20 years or more before this question is finally resolved," Hales said.
At this point you may be wondering why one would not simply build a foam out of equal-volume bubbles and look at the configuration it forms. In fact, over the years many have tried the experiment. Until recently, the best known of these efforts were experiments conducted in the 1940s by the physicist Edwin Matzke, who created a foam of 1,900 bubbles one bubble at a time, using a syringe. At the end of this laborious procedure, he examined 600 bubbles at the center of the foam. Matzke found that the average number of sides belonging to each cell was very close to 14 (the number of sides of Kelvin's truncated octahedron), but he did not find a single copy of Kelvin's cell. In fact, he did not discover any ordered pattern at all. In an amusing address in 1950 to the Torrey Botanical Club at Columbia University, he warned of the dangers of leaping from mathematical models to real-world conclusions "in the twinkling of an eye."
For many years, Matzke's experiments appeared to have closed the subject. Weaire and Phelan, however, suspected that his observations were misleading. Matzke's method for creating a foam was so time-consuming that often a full day elapsed between the creation and the measurement of a bubble. This opened the door to serious errors, because as time passes, air tends to leak across foam walls from one bubble to another, altering their size and shape. Weaire and Phelan decided to try the experiment anew, and they built a foam using the time-honored and speedy method of blowing bubbles through a straw. They found several of Kelvin's cells near the surface of the foam and, deeper inside, several small fragments similar to their own structure. Weaire and Phelan observed that "with the benefit of hindsight, it would appear that the subject has suffered in the past from an excess of theorizing and a shortage of experiments." As techniques for building foams are refined, it may be hoped that they will produce clearer and clearer pictures of the structures that nature chooses for its foams.
The overthrow of Kelvin's partition by a less symmetric, more complicated structure came as an intriguing, somewhat disturbing piece of news to scientists who believe that the best configuration should display beautiful symmetry. However, the Weaire-Phelan structure may enjoy only temporary status as the optimal foam structure. We should recall Penrose's dictum: When to us the contest may appear to be between two well-understood possibilities, nature may suddenly pull out of its hat a completely different and infinitely more elegant solution.
© Erica G. Klarreich
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.