American Scientist

The essential change implicit in the arrow in a chemical reaction, A + B → C + D, may be rapid, it may be slow. I drop a small chunk of potassium into water, and the show is over in less than a second. The majestic copper beech outside my window was not noticeably smaller yesterday, but a photograph of it 75 years ago shows it just 10 feet high. Many biochemical reactions went into that slow growth. They tell me the universe is 15 billion years old, they tell me that the primary photochemical act in vision—a change in shape of a retinal molecule—transpires in 200 femtoseconds. (One femtosecond, fs, is 10^–15 seconds—the name of the unit a relatively rare intrusion of a nice Scandinavian root into a scientific nomenclature generally too anxious to impress in Greek and Latin.) I sort of trust the former, I believe the latter, and in this third Marginalia on the new kinetic chemistry, I would like to tell you why.

When events happen in the time frame defined by our senses, we can easily gauge their rapidity. We have no trouble hearing the difference between a pulse rate of 55 and 155 beats per minute. And we can make out, a bit less distinctly, the number of years elapsed between a frame of Ingrid Bergman in her early Intermezzo and late Autumn Sonata. But as we move to shorter and longer time intervals we must abandon the direct and sometimes fallible evidence of the senses and rely on instruments and theory.

Snappy Shots

Let's talk about very quick chemical reactions, those seemingly over before the eye blinks. It seems obvious that if we are to understand them, we must take a quick series of snapshots. How naturally we lapse into the language of photography! Since the end of the 19th century the technology has been in place for producing still images separated in time by intervals much shorter than the eye can resolve. So Étienne-Jules Marey in 1894 showed us sequences of a cat righting itself as it falls. Earlier still, in 1878 Eadweard Muybridge set up a dozen cameras along a track, trip wires opening their shutters for two-thousandths of a second. Leland Stanford's bet that all four hooves of a horse are off the ground at some point in a gallop was thus proved. And in our century, Harold E. Edgerton's strobe flash caught a bullet passing through an apple.

A little thought about each of these photographic experiments reveals that they depend on signals (typically light at some frequency), a device for recording them (a photographic film), and most important, a precisely sequenced timing of two or more events (the trip-wire, stroboscopic lighting). Muybridge's "experimental setup" would not have resolved Leland Stanford's bet unless the trip wires indeed tripped the shutters expeditiously, the shutter speed were short enough to define the horse and the light level were sufficient to record the event on the film used. The circumstances of the measurement—the distance between the trip wires, the shutter speed, the light—all had to be matched to the speed of the galloping horse, so to say. A similar setup would teach us nothing about the bullet and the apple.

In the experiments I will describe below, people "freeze" the pieces of a molecule as bonds form or break up in the course of chemical reaction, or as the molecule is perturbed in some way. A typical bond length is 1.5 angstroms (?; 1? = 1 x 10^–10 meters), and we might want to see it changed to 2.5 ?. This in a reaction where the formerly bonded pieces might be going off at speeds something like 1,000 meters per second (m/s) relative to each other. How long does it take for the molecular fragments to travel 1 ?? Only 1 x 10^–13 s, or 100 fs. Light pulses that could freeze such motion had better be well defined, and in duration substantially shorter still.

The reason I speak of pulses is that this is the way it must be done if we are to learn something of molecules reacting—more in the spirit of Edgerton's stroboscope than Muybridge's trip wires. There is as yet no mechanical shutter that can open or close on the femtosecond time scale, nor can a photographic film form images of angstrom-level resolution. The logic of the experiments I will describe is that of the interaction of short, precisely timed pulses of light with matter.

Pump and Probe

Still another piece of the logic of femtosecond experiments is the pump and probe technique. Two bursts of laser power are required; the first pumps the molecule, excites it, starts the reaction going. A precise and precisely variable time thereafter, the second pulse probes the action.

As in comedy, it's all about timing. Often the pump-and-probe pulses are sent on their appointed rounds at exactly the same time; that is easy to arrange. But the probe pulse light is routed a longer way. "Longer" doesn't mean much longer; the velocity of light is 3 x 10⁸ m/s, so a 3.3-fs delay is caused by a path difference of only 1 x 10^–6 m, one-thousandth of a millimeter. Can one arrange such a precise path-length difference for the pump-and-probe pulses? No sweat, at least today. You can't do it on top of a New York subway grate, but the same kind of piezoelectric controls that in scanning tunneling microscopy move a tungsten tip a few angstroms left or right serve in this case.

Power

Whatever the pump pulse does, it does it for a very short time. It better do its controlled violence with substantial power, or there will be nothing for the probe pulse to probe. The output of a modern femtosecond-pulsed laser used in one of the experiments described below is 75 millijoules (mJ) in 20 fs. Were it to operate continuously for one second, this laser would require 3.75 ? 10¹² joules of energy. The same energy would keep all of Milan, Italy—residential and industrial—lit up for more than one hour. No amount of funding, no power station will provide power at that rate—for that matter, were the laser output continuous the sample (maybe the lab) would be consumed in a mighty flash in no time (well, in some microseconds)!

Useful Uncertainty

Heisenberg's uncertainty principle places an inherent limitation on the simultaneous determination of certain pairs of physical observables—momentum and position, energy and time. Might the principle constrain our "visualization" of the location in space of, say, moving atoms? Actually, it doesn't; the localization in time allowed by coherent, ultrashort laser pulses indeed leads to a substantial indeterminacy in the energy. This in turn is related to an inability to define well the momentum of the particles in motion, which actually leads to a good coherent localization in space. I oversimplify a complex and interesting quantum-mechanical situation. A language of matter wave packets is necessary, but in that language we can actually think of atoms, which are very much quantum objects, moving as roughly classical particles.

The Intermediate Detected

Ahmed Zewail of the California Institute of Technology has provided us with many of the concepts of femtochemistry, exemplifying them through a series of beautifully designed experiments. I mention here but one of them, relevant to a kind of organic reaction of interest to me.

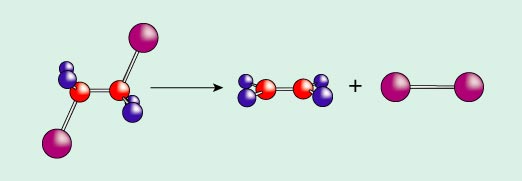
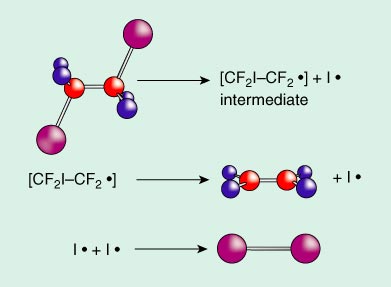
On photolysis, halogen-substituted ethanes fall apart to ethylenes and diatomic halogen, X₂ (X is iodine, I, in the case studied). The overall reaction is shown in Figure 2. But how exactly does this happen? Does the reaction proceed in one fell swoop, the iodine atoms coming off in a concerted manner? Or is there an "intermediate," as in the mechanism shown in Figure 3? The geometrical details of the CF₂I–CF₂ are left undefined, as they were when the experiment was first done.

Zewail and coworkers showed unambiguously that the two C–I bonds do not break synchronously. Furthermore they defined for us the time scales of the various processes. First one C–I bond is broken, in approximately 200 fs. This is followed by a much slower cleavage of the second C–I bond, in about 32 picoseconds, which equals 32,000 fs.

The Intermediate Identified

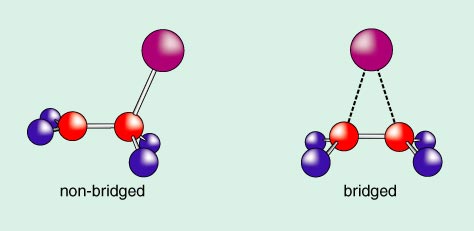
You will note above that the femtosecond-scale spectroscopy identifies the intermediacy of a specific molecule (CF₂I–CF₂) with a certain lifetime. But what is the structure of that molecule? From experience with related molecules, one could imagine the intermediate "non-bridged" (in the position of the I) or bridged, as shown in Figure 4.

For stable molecules, especially those forming nice little crystals, we have a marvelous technique, x-ray crystallography, to determine the structure. Nuclear magnetic resonance, electron diffraction and microwave spectroscopy also give us geometrical information. But imagine the problem of applying these techniques to a figurative handful of molecules zooming around in high vacuum!

In the most exciting development in recent years, people are beginning to do just that. In January 1999 Jianming Cao, Hyotcherl Ihee and Zewail published an electron diffraction study on CF₂I–CF₂ in situ, pointing to a non-bridged structure for the intermediate. And in a remarkable paper that is in a March issue of Nature, Kent R. Wilson of the University of California at San Diego and his group succeeded in following a structural change on the femtosecond scale by x-ray diffraction.

Here's what the San Diego chemists do. They illuminate the surface of a crystal of gallium arsenide (GaAs) crystal with 800-nanometer laser light. This creates electron-hole pairs in the semiconductor. The electronic excitation is quickly transformed into heat, and the heat wave at the surface dissipates into the interior. The structural change at the GaAs surface may be complex, but its most important component is simply heat-induced expansion of the lattice.

That expansion is probed by x rays generated at a copper wire by that 75-mJ, 20-fs laser pulse that was energetic enough to light up Milan. What one sees very clearly in Figure 5 is a motion of a crucial x-ray reflection, a function of the lattice spacing, as the surface is heated. Corresponding to an expansion at the surface of only 0.0082 ?.

Not much that is surprising, you will say; the structural information is meager, the molecules small. But Kent Wilson's x-ray observations, as Zewail's electron diffraction, are proof-of-principle experiments. I think within the next decade we will see ultrafast structural studies defining precisely the many transient species we now know exist but whose identity is so far hidden from us.

© Roald Hoffmann

Acknowledgment

I am grateful to Dick Zare, Debra Rolison and especially Paul Houston for their comments on this article, and to Pradeep Gutta for producing the molecular models in these illustrations.