American Scientist

More than a century after his death, the name of Daniel Kirkwood continues to be familiar to almost any student who takes an elementary astronomy course. There the student learns that asteroids are mainly located in a belt between the orbits of Mars and Jupiter, and that Kirkwood discovered there is a succession of gaps in that belt where no asteroids are found. This discovery made him justly famous, and it is still a staple of elementary texts and research papers alike. But ask any student—or instructor—what else Kirkwood was famous for in his own time, and you will likely be met with a puzzled frown and shake of the head. Tell them that long before the "gap" discovery, he made another that brought him worldwide attention and had prominent astronomers and the popular press hailing him as the equal of Johannes Kepler, and you will likely receive a skeptical smile. But it was so.

Adding to the extraordinariness of this event was Daniel Kirkwood's background. He was born in 1814 on a Maryland farm, and his only education as a child came from the local country school. At the age of 19, having no taste for farming, he became a schoolteacher in another such country school. One of his students wished to study algebra, and since Kirkwood knew none, he and the student sat down and worked through an elementary textbook on the subject together—a rather unlikely beginning for one who later held the chair of mathematics at a major university. From this Kirkwood realized that he had both a flair and a taste for mathematics and so went back to school himself for several years to study it. By 1849 he had worked his way up from being a mathematics instructor to become principal of an institution called the Pottsville Academy of Pennsylvania. It was about this time that he made his discovery.

During these years of development and reading, Kirkwood had slowly become intrigued by the fact that, although there is a law governing the revolution of planets (Kepler's third law), no law had as yet been discovered governing their rotations. (Astronomy makes a distinction between the terms rotate and revolve; a body rotates about an axis within itself but revolves about an axis that is exterior. Thus the earth rotates once a day but revolves about the sun once a year.) Kepler's third law of planetary motion says that if P is a planet's period of revolution about the sun, and d is its distance from the sun, then P² is proportional to d³. Kirkwood spent some 10 years off and on mulling over what might be a corresponding law governing planetary rotations, but with no success.

Eventually, in August of 1846, a study of Laplace's theory for the origin of the solar system led him by a process that is not at all clear to the following proposition. Consider three consecutive planets lined up in a row. There will be a point between the middle and outer planet at which a particle will experience equal gravitational force from the two planets, and another such point between the middle and inner planet. Calculate the distance, D, between these two points, the diameter of the middle planet's "sphere of attraction." Next, from the known periods of rotation and revolution calculate the number of rotations, n, that a planet makes in the course of one revolution. Kirkwood's calculations suggested to him that n² was proportional to D³ as one went from planet to planet. He referred to his result as the analogue of Kepler's third law.

Unlike some who think they have discovered an important scientific law (Kepler himself, for instance, prancing around in paeans of ecstasy as to how God had waited 6,000 years for someone to discover what Kepler thought to be celestial harmonies among the planets), Kirkwood's behavior was exemplary. He wrote in very modest fashion to Edward Herrick at Yale, describing his discovery but noting that "perhaps it may be regarded by those better qualified to judge than myself, as a vagary not worthy of consideration." Herrick suggested that he send his letter to an astronomer at the U.S. Coast Survey, Sears Walker, then well known for his work on Neptune's orbit. Walker discussed the finding with other members of the American Philosophical Society and soon became an enthusiastic advocate, announcing that it "deserves to rank at least with Kepler's harmonies." In August 1849 Walker presented Kirkwood's letters to a meeting of the American Association for the Advancement of Science (AAAS), again concluding the result to be "the most important harmony in the solar system discovered since the time of Kepler, which, in after times, may place their names, side by side, in honorable association."

The AAAS members were impressed. Benjamin Peirce, doyen of astronomy at Harvard, declared it to be "the only discovery of the kind since Kepler's time, that approached near to the character of his three physical laws." Benjamin Gould, founder of what became one of the world's most important astronomy journals, said "I do not wish to express myself strongly . . . [but] nor can we consider it as very derogatory to the former to speak hereafter of Kepler and Kirkwood together as the discoverers of great planetary harmonies." Newspapers and journals soon brought the public to know of this wonderful and amazing discovery.

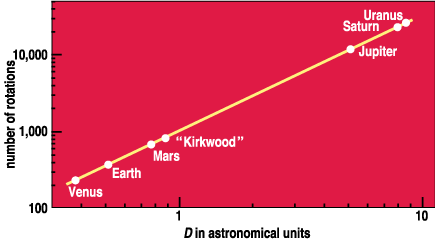
Walker, it would seem, was carried away by his own enthusiasm. He submitted a letter to the editor of the prestigious German journal Astronomische Nachrichten outlining "the discovery [as] thus announced by Mr. Kirkwood." It is only one-and-a-half pages long and contains only one table. The final column in this is labeled "Kirkwood's diameter of the Sphere of attraction, D," derived, one would assume, from the observational data listed in previous columns of each planet's distance from the sun, mass and rotational period. But if one uses these data to compute the period of revolution by Kepler's third law and thus n for each planet, and plots that against D, one obtains the graph shown in Figure 1. The straight line has the equation n = 1000*D^1.5 and is an amazing fit of the line to the points! Especially when, as we now know, some of the input data were wildly wrong. The mass of Mercury, for instance, was wrong by more than a factor of 2, Venus's rotation period was in error by more than a factor of 200, and most of the other data were somewhat in error. What was going on?

Planet Kirkwood

The fact is that the statistics were really pretty sparse. Because Mercury has no planet between it and the sun, and Neptune in Kirkwood's time had no known planet beyond it, neither could have a D value calculated for it (although their masses entered into the D values for Venus and Uranus respectively). Moreover, since there is no major planet between Mars and Jupiter, although the asteroids are there and the curious Titius-Bode relation predicts a planet there, one cannot determine D for either Mars or Jupiter. That left Venus, Earth, Saturn and Uranus. The rotational period of Venus (and thus n) was essentially unknown at the time, but vague markings seen telescopically suggested a period near one day, and, Venus being consistently referred to as Earth's "sister" planet, that was the value used by Walker and probably Kirkwood. (It is, in fact, 244.3 days, and the rotation is backwards to boot!)

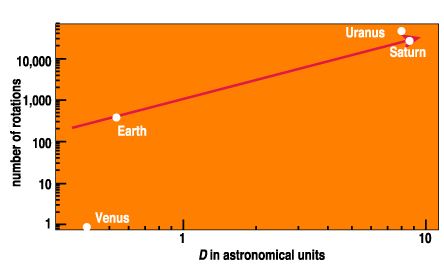
With so little to go on, Walker adopted a two-stage procedure. He ingenuously explained how he first used the data for Venus, Earth and Saturn to determine a preliminary relation between n and D. He then used that relation to work backward and establish that the supposed planet (named "Kirkwood" by Walker), which was thought to have broken up to produce the asteroids, must have been 2.908511 times the earth's distance from the sun, had a mass of 0.262290 earth masses and a rotational period of 2.23904 days. With that established he could then calculate D for Mars, "Kirkwood" and Jupiter, and include them in the n-D relation. Furthermore, this procedure also resulted in Walker's "slight modification" of three other masses, and so, in the end, the marvelous results seen in Figure 3. Surprise! Surprise! No wonder that those like Gould and Peirce, who perhaps never delved into the details, were extreme in their praise of these findings. Figure 4 shows what one gets using today's input numbers and restricting oneself to just Venus, Earth, Saturn and Uranus. Not nearly as exciting! As for the putative planet "Kirkwood," it is now virtually certain that no such planet ever existed. More likely the powerful gravity of proto-Jupiter prevented smaller bodies in that region from coalescing into a full-blown planet in the early stages of the solar system, resulting in only a belt of asteroids.

Cool Reception

Across the Atlantic, with the element of national pride removed, there was less enthusiasm than in the U.S. On the one hand, David Brewster in his 1850 presidential address to the British Association for the Advancement of Science applauded Kirkwood's discovery as a work of genius. On the other hand, Heinrich Schumacher, editor of the Astronomische Nachrichten, where Walker had published his letter, declined comment on the subject beyond a scathing note suggesting that readers could judge for themselves "how much . . . is really factual and how much is simply hypothetical." Most European astronomers seem to have sided with Schumacher, if, indeed, they commented on the matter at all.

Eventually, however, all the high praise died down, and, it seems, less and less was heard about Kirkwood's analogy, until today it is all but completely forgotten.

Still, Kirkwood received an honorary doctorate from the University of Pennsylvania in 1852 and appointment to the chair of mathematics at Indiana University in 1856, events that one presumes probably would not have happened without all the previous praise and publicity.

For one so modest and diffident, it is remarkable that the setback in fortune of the n-D relation did nothing to dissuade Kirkwood from publishing later research. Three books and well over 100 papers came later. The most famous paper was published in 1866 when he examined the statistics of the 80 or 90 asteroids then known and found that essentially none of them was located where its period of revolution about the sun would have been a simple fraction (one-half, one-third, three-fifths etc.) of Jupiter's period. These were the now-famous gaps in the asteroid belt. Kirkwood recognized that asteroids in such resonances would encounter the full effect of Jupiter's pull more frequently than otherwise, and so were soon removed from those positions. In fact, he realized more sophisticated effects were present as well, and, indeed, research on the subject has continued into our own times. Kirkwood also pointed out the same year that the main gap in Saturn's rings (Cassini's division) is owing to the same phenomenon: Ring particles at that location would have one-third the period of the satellite Enceladus and nearly one-half that of Mimas. In 1861 he gave the first convincing evidence of a connection between meteor showers and comets, and over the years made several other solid contributions to solar-system science.

So in the end Kirkwood could look back on a very satisfactory career, even if he wasn't the American Kepler. He retired to California in 1886, becoming for a while an astronomy lecturer, aged 77, at Stanford University, and eventually died in 1895 a few months short of his 81st birthday. His friend and former colleague, Joseph Swain, said of him at the time of his retirement that "during his fifty years as a teacher, he has gained from his students such universal love and admiration as few men can enjoy, and while ? he has made many valuable contributions to science, as a genial, temperate, and genuine man, he has solved the problem of gracefully growing old." Kepler should have been so lucky.

© J. Donald Fernie