American Scientist

The word boson causes no end of trouble when people report on the discovery of the Higgs boson, the master particle that allows the other fundamental paticles to have mass. It regularly gets pronounced “bosun,” and once, while being interviewed on TV, I saw it spelled as “bosom.” To clarify: Boson is the name for a generic class of particles. The Higgs boson is one, but so are many other particles. In the current Standard Model of particle physics, all the particles that carry forces—gluons (strong nuclear force), the W and the Z (weak nuclear force), photons (electromagnetism), plus the graviton (gravity), if there is one—are bosons.

Quarks, electrons, and neutrinos, on the other hand, are fermions. (Quarks are the constituent particles of protons and neutrons.) The difference between them is just spin. But in this context, spin is a quantum of angular momentum. It is a bit like the particle is spinning, but that is really just an analogy, because pointlike fundamental particles could not spin, and anyway fermions have a spin such that in a classical analogy they would have to go round twice to get back to where they started. Quantum mechanics is full of semimisleading analogies like this.

Regardless, spin is important. Bosons have, by definition, integer spin. The Higgs has zero; the gluon, photon, W and Z all have one; and the postulated graviton has two units of spin. Quarks, electrons, and neutrinos, as fermions, all have a half unit of spin. This distinction causes a huge difference in their behavior.

The best way we have of understanding fundamental particles is quantum field theory. In this theory, a state is a configuration describing all the particles in a system. The mathematics is such that if you swap the places of two identical fermions, with identical energies (say, two electrons), then you introduce a negative sign in the state. If you swap two bosons, there is no negative sign.

Because swapping two identical particles of the same energy makes no physical difference to the overall state, you have to add up the two different cases (swapped and unswapped) when calculating the actual probability of a physical state occurring. Adding the plus and the minus in the fermion case gives zero, but in the boson case they really do add up. This means any state containing two identical fermions of the same energy has zero probability of occurring, whereas a state with two identical bosons of the same energy has an enhanced probability.

This fairly simple bit of mathematics is responsible for the periodic table and the behavior of all the elements. Chemical elements consist of an atomic nucleus surrounded by electrons. Because electrons are fermions, not all the electrons can be sucked into the lowest energy level around the nucleus. If they were, the probability of that state happening would be zero, by the argument above. So as more electrons are added around a nucleus, they have to sit in higher and higher energy levels—less and less tightly bound to the nucleus. The behavior of a chemical element—how it reacts with other elements and binds to form molecules—is driven by how tightly bound its outermost electrons are.

When bosons clump together they do some fascinating stuff too. The condensate they form is responsible for the superconductivity in the magnets at the Large Hadron Collider (LHC), where we found the Higgs. But it’s hard to beat being responsible for the whole of chemistry, and therefore biology. Some theories extend the Standard Model by relating force-carrying bosons to matter–particle fermions. They do this by introducing a new symmetry between them. This symmetry is so mathematically compelling that it is called “super”—supersymmetry.

Reasons for Supersymmetry

For a variety of reasons it is not possible to discuss LHC physics for long without talking about supersymmetry. It is a bit weird that there have been 21 annual supersymmetry meetings, even though there is as yet no experimental evidence for supersymmetry playing any role in actual particle physics. Perhaps it’s excusable. At least before the LHC switched on, supersymmetry was arguably the best way to improve the Standard Model of particle physics.

Recall that all the matter particles (quarks and leptons) are fermions, and all the forces are carried by bosons. You might (especially if you are a physicist) ask whether this is really a rule of nature, or a coincidence. What if you swapped all the bosons and fermions over, would the world be very different or not? This is a very good question, by which I mean that asking questions similar to this has led us over the years to some very important and interesting answers. It is a symmetry question. Symmetry is probably the single most important concept in physics. One of the most important theorems we have, which applies to the classical and quantum regimes of physics, is Noether’s theorem, named after mathematician Emmy Noether. This states that for every continuous symmetry in nature, there is a conservation law.

Although symmetry is firmly established as a useful principle in physics—and in particle physics in particular—supersymmetry has yet to prove itself. Why, then, have there been (at the time of writing) 21 conferences on the topic? As far as I can see there are three big arguments in its favor: It helps with an important problem in the Standard Model. It sort of predicts dark matter, the invisible mass component of the universe. It looks nice.

The Standard Model of particle physics is clearly not the full story, there still must be something beyond it.

• Facebook
• Twitter

The first of these reasons has to do with the Higgs boson. Unlike supersymmetry, the Higgs boson is an integral part of the Standard Model, without which it doesn’t work. There is a subtle problem with this, though. Because the Higgs boson, uniquely amongst all Standard Model particles, has no spin, its mass picks up a particular kind of quantum correction. If left alone to do their thing “naturally,” these quantum corrections tend to make the Higgs boson millions of times heavier than it has to be in the Standard Model.

This was (and is) a real worry for the credibility of the theory. From one point of view, it makes the Standard Model look like a coincidence on the level of one in ten thousand million million. This is about a hundred times less likely than winning the lottery jackpot two weeks running if you buy a single ticket each week. Supersymmetry gets around this because fermions give negative corrections and bosons give positive ones, so if there is an (even approximate) symmetry between the two, most of the corrections cancel each other out and the Higgs mass can be sensible without fine-tuning things to achieve such a crazy coincidence.

The second argument is to me the most compelling. Astronomical observations tell us there is probably some dark matter out there (or else we really do not understand gravity). Many supersymmetry models predict a particle that would be an ideal candidate for dark matter. It may be right behind you. When two different branches of science have problems that seem to converge on the same solution, look out for progress.

The third argument is essentially the fact that supersymmetry is a way of pushing ideas about symmetry, which have been shown to be a great way of understanding nature, even further. There are two types of symmetries (technically, the Poincaré group of external, space–time symmetries, and internal symmetries such as charge), and there is a theorem that states that external and internal symmetries cannot mix up with one another. Internal symmetry operations turn one kind of particle into another (for example, the matter–antimatter symmetry operation turns electrons into positrons), whereas external symmetry operations move you around in space–time (for example, the translation symmetry operation just moves an electron to a different place). But swapping a boson for a fermion does both, because although it obviously turns one kind of particle into another, it also involves a space–time transformation, because spin is actually angular momentum.

Supersymmetry is therefore a special loophole in the theorem that says internal and external symmetries can’t mix. In fact it is the only such loophole in a four-dimensional theory such as the one we need to describe our universe. Because all the other available symmetries are exploited in nature, with elegant and far-reaching consequences, it is very attractive to suppose this last available symmetry should appear too.

Those are three quite strong reasons for taking supersymmetry seriously. But they all have their weaknesses too. For the first one, maybe the universe just got lucky? Or maybe we’re missing something subtle in the Standard Model that might force these cancellations, so they happen without that fine-tuning, a bit like cheating on the lottery. For the second of those reasons, well, there are other theories that can also produce dark-matter candidates. And for the third, we know that many beautifully symmetric mathematical ideas have wrecked themselves on the rocks of data. We shall have to wait and see.

The Big Announcement

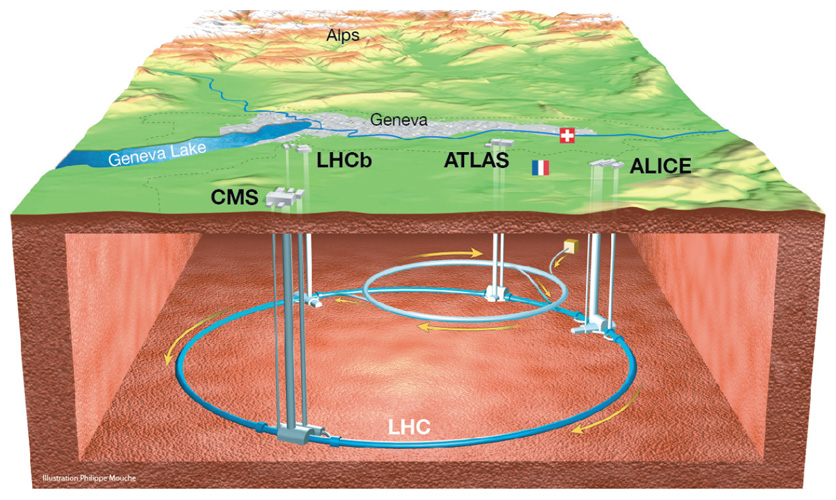
The crucial moment for me, for the LHC’s ATLAS detector where I worked, and for the LHC as a whole started on July 3, 2012. I was in Salle Curie, one of the conference rooms below Building 40 at CERN. There are four of these rooms, and the weekly meetings of the Standard Model group were usually held in Salle Curie. However, this morning Fabiola Gianotti, the spokesperson (meaning boss) for ATLAS, would be rehearsing a talk. It was entitled, with studied neutrality, “Status of Standard Model Higgs Searches in ATLAS.” It would be given on the morning of the following day, with a webcast around the world.

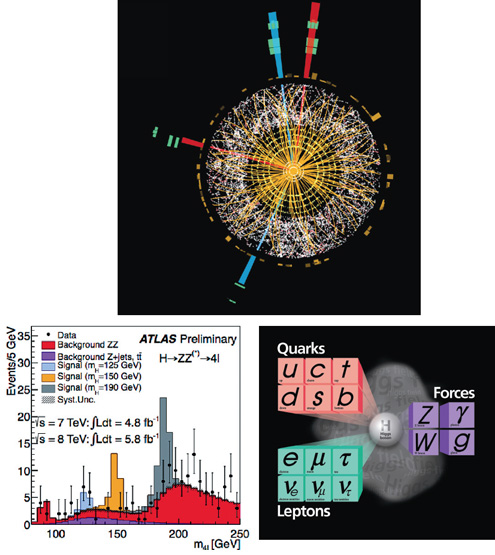
It had become increasingly clear, initially to us and gradually to the media, that this was likely to be the big one. But even knowing what was coming, the moment when Fabiola showed our data, and our conclusions, hit me hard. I had seen some of the slides already, and the documentation and analyses behind them. These were the work of hundreds of colleagues, many of them more directly involved than me in this particular analysis. Years and years of work lay behind the results. Seeing Fabiola declare to all of us what we had done was surprisingly emotional.

At the end of the talk, we decided to stop calling it an “excess of events” and call it a new boson. After all the rumors and the hints, all the projections and the hows and whys, finally we had, beyond reasonable doubt, discovered something fundamentally new. Pretty much anything could in principle have turned up at the LHC, because no one had done this before. But if the Higgs boson had not shown up, our understanding of fundamental physics, as encapsulated in the Standard Model, would have been shown to be incomplete. Well, let’s be frank, it would have been wrong.

The chain of reasoning is amazing. We knew that the origin of mass occurs at LHC energies. We knew this because two fundamental forces, electromagnetism and the weak nuclear force, unify at these energies. The reason these forces look different to us in everyday, low-energy life is that the force-carrying particles for the weak force, the W and Z, have mass and the photon does not. We had, in the Standard Model, come to the conclusion that this mass can only happen if a certain kind of quantum field fills the universe and sort of sticks to some particles to give them mass.

That is indeed quite an extreme leap to make, based on some fairly esoteric mathematics. The only way of proving whether we’d done the right thing or not, whether the field is real or not, was to make a wave, an excitation, in the field. This wave is, or would be, the Higgs boson. And it has to show up at the LHC or the field is either not there or is very different from what we expected. There was nowhere to hide.

Inventing a whole-universe-filling field to make your math come out right is pretty radical. But it was looking as though it might just have worked. On July 4, 2012, we had seen something fundamentally new, which fit the description of the particle predicted by mathematical understanding of previous data, coupled with some prejudices about aesthetics, symmetry and how a decent universe ought to hang together. I don’t know about you, but this still amazes me.

Where Do We Go from Here?

As I write this, the restart of the LHC with higher-energy beams for physics is expected early in 2015—April 1, in fact. One thing we will definitely do with that upgraded LHC, and hopefully with other machines, too, is examine very closely how well the Standard Model works above the electroweak symmetry-breaking scale. This energy regime is qualitatively different from anything we have looked at before.

In this regime, the electromagnetic and weak forces are in some sense unified. Certainly their strengths are now comparable. Without the discovery of the Higgs boson, this would have been a no-go area for the Standard Model. The theory would have been unable to make predictions for these energies, and would have been relegated to a low-energy “effective theory,” stunningly accurate for energies below a couple of hundred GeV (billion electron volts), but out of its depth above the electroweak symmetry-breaking scale.

With the discovery of the Higgs, the Standard Model has a new lease of life. It can make predictions for very high-energy physics, covering everything even an upgraded LHC is able to reach. This is a bold claim, and putting it to the test will be intriguing. One area I find fascinating is the theoretical activity stimulated by the fact of observing a new boson with a definite mass. A lot of this work is very technical, but one general theme is a re-examination of symmetries and quantum corrections already in the Standard Model to see if they contain more physics than we first thought.

There are all kinds of (possibly misleading) clues scattered around and games that can be played. For example, consider a numerical coincidence. The sum of the masses squared of the fermions is very close to the sum of the masses squared of the bosons. To put it another way, if you had found a symmetry that imposed a condition that the sum of the fermion masses must equal the sum of the boson masses, you could have predicted a Higgs mass of about 123 GeV. Not too far off what we have measured!

The catch is that there is no symmetry we know of that imposes this, so at present it is just a curiosity. There are other ways one could make “predictions” or hunt for coincidences, and the more ways of looking for a coincidence, the less significant a coincidence is if you find it. Look a million different places, and you’ll probably find a million-to-one chance turning up. Equally, although a bit of numerology might give a clue, it is only useful if it is a clue to a real dynamical theory. The way to go is to make measurements and do real calculations, not play number games.

The LHC data, from the LHCb experiment and CMS (two other LHC experiments) as well as ATLAS, have ruled out huge swathes of previously possible variants of supersymmetric theories. Yet despite this, as an idea supersymmetry is never likely to go away. The beauty and elegance of the mathematics behind it, coupled with the fact that it is required by string theory, or M-theory, or most likely any other attempt to bring gravity and quantum field theory together, will ensure, I guess, that it remains an important part of the toolbox of theoretical physics, cosmology and mathematics more or less indefinitely.

What is at stake is whether supersymmetry has anything to do with electroweak symmetry-breaking, or with dark matter, or indeed whether it has anything to do with any phenomenon ever likely to be measured in a particle-physics experiment. And supersymmetry is only (currently) the most popular extension to the Standard Model. Cock-a-hoop though the Standard Model may be with its latest success in predicting a fundamental scalar boson and extending its region of applicability well above the electroweak energy scale, the Standard Model is clearly not the full story. There still must be something beyond it, supersymmetry or no.

The most glaring omission is gravity. We have, thanks to Einstein, a very good theory of gravity, but it is not a quantum theory. Space–time is the stage on which quantum field theory plays its part, but at some high energy the idea of a classical space–time comes into conflict with quantum field theory, and we don’t know what happens then.

Other problems and omissions include the small point of the missing 85 percent or so of matter in the universe—the dark matter that is visible only by its gravitational effects on galaxies and other astrophysical objects. Is it a new fundamental particle? It certainly doesn’t seem to be explainable by any Standard Model particle. Worse, there is dark energy, which makes up 68 percent of the stuff (matter plus energy) in the universe. From one point of view, dark energy is just a label for the fact that the rate of expansion of the universe is increasing, for reasons that are unclear.

While we are at it, why are we made of matter and not antimatter? And why are there three copies, three generations, of the fundamental particles? And why does the weak force see only particles with left-handed spin, ignoring the right-handed ones? And then what about the neutrinos in all of this, and why are they so light when the top quark is so heavy?

There are a lot of seemingly arbitrary features of nature here that, to a certain type of mind (e.g. mine), plead for a more elegant explanation than "just because." The LHC, and particle physics more broadly, has a lot on its plate.

(Excerpted from MOST WANTED PARTICLE: The Inside Story of the Hunt for the Higgs, the Heart of the Future of Physics, copyright © Jon Butterworth 2015. Reprinted by permission of the publisher, The Experiment.)