
This Article From Issue
May-June 2020
Volume 108, Number 3
Page 186
THE ART OF STATISTICS: How to Learn from Data. David Spiegelhalter. 426 pp. Basic Books, 2019. $32.
Can statistics be understood without mathematical formulas? Yes, up to a point. The Art of Statistics: How to Learn from Data, by David Spiegelhalter, is an introduction to the study of data and statistics for interested readers; it resembles in some ways an introductory textbook but is much less formal. The book emphasizes basic concepts and tools of data representation and leaves out the algebra.
Spiegelhalter has chosen to begin his book not with lessons on probability theory but with exemplary instances of reasoning with data. In an initial example, he discusses the case of an English physician, Harold Shipman, who in 1999 was convicted of murdering 15 of his patients. After the trial, Spiegelhalter and other statisticians were asked to conduct an inquiry into what additional crimes Shipman might have committed. They eventually determined that he had actually murdered at least 215 (mostly elderly) patients over a period of 24 years. Spiegelhalter shows that an exploration of the data regarding the patients who died reveals patterns that lead to insights into Shipman’s behavior (see scatterplot below). In a subsequent example, Spiegelhalter examines ship records from the Titanic to identify the combination of passenger characteristics associated with the highest rates of survival; the most favored passengers were women and children with first- or second-class tickets. In each of these examples, he creates visual displays of data to uncover patterns that are specific to these cases. Because there is no effort to generalize beyond the case at hand, calculations of statistical error are not relevant.
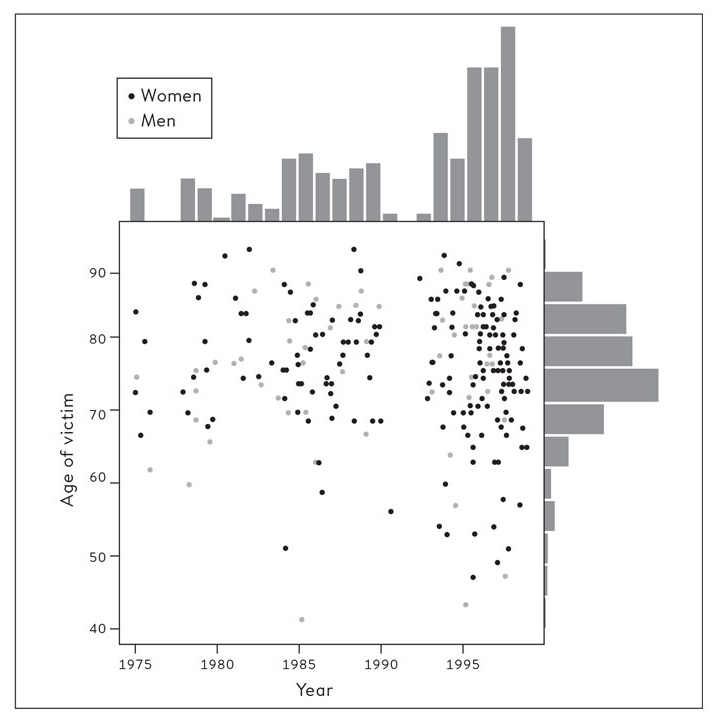
From The Art of Statistics.
Yet another of Spiegelhalter’s cases involves an English hospital’s elevated death rates for heart surgery on children. Here the question is whether these bad results are attributable to insufficient experience with this type of surgery at the hospital in question. In this case he would like to generalize, and for a variety of treatments, the candidate explanation of too little specific experience with the surgery is accepted by many. But a statistical calculation of error can scarcely be relevant unless the patients brought to different hospitals can be taken to be comparable. There are good persuasive reasons to think that they are not comparable, and in that case a probability calculation would count for little.
Alfred Kinsey, who created a sensation with his American statistics regarding sexual behavior, made no effort to get representative data. Accurate data on sexual behavior are needed for various reasons, including prediction of the spread of sexually transmitted diseases. In the United Kingdom, the National Survey of Sexual Attitudes and Lifestyle (Natsal) was created to obtain such data, and it has been carried out once per decade since 1990. Spiegelhalter discusses some of the results of the 2010 Natsal survey—specifically, the number of lifetime sexual partners reported by people aged 35 to 44 years. The data show obvious anomalies, including higher numbers of reported sexual partners for men than for women and distributions with pronounced peaks at multiples of 10. Statistics as a data science often begins with sometimes tricky problems interpreting data.
Not until page 205, more than halfway through the book, does Spiegelhalter take up the topic of probability theory. Immediately he credits the founding of statistics to a pair of mathematicians, Blaise Pascal and Pierre de Fermat, on the basis of their correspondence in the 1650s on the calculation of odds in games of chance. Singling out combinatorial probability as a unique point of origin can scarcely be reconciled with the perspective of Spiegelhalter’s book. Political arithmetic, for instance, which took off later in that century, addressing issues of population, mortality, and wealth, is at least as plausible a candidate. Another is the introduction and systematization of census taking toward the end of the 18th century. The word statistics refers to a state science—or science of statecraft—that came to be associated principally with numbers in the 1830s. We might also think of the accumulation and analysis of astronomical and meteorological data. Topics such as these were long central to statistics. With the emergence in about 1930 of a more mathematical version of statistics, this wider field of study tended to fade into the shadows, but it has never disappeared. If anything, it has expanded. Spiegelhalter’s book acknowledges and even emphasizes the decisive importance of diverse forms of data work for present-day statistics. It is time now to recognize their central role in statistics across the wide sweep of history.
Leaving aside his Pascal-Fermat creation story, Spiegelhalter’s historical perspective on statistics mainly sets off from the English biometricians Francis Galton and Karl Pearson, both of whom treated it as a wide-ranging data science. Pearson, more than Galton, emphasized also the calculation of error as a standard for deciding whether an apparent effect should be accepted as real. Beginning in the late 1910s, another English mathematician, Ronald A. Fisher, reformulated statistics as rules of experimentation, the basis of scientific inference. As Spiegelhalter explains, these methods were bitterly contested almost from the start, especially by Jerzy Neyman and Pearson’s son Egon. These rival versions of statistics, Spiegelhalter emphasizes, were never reconciled, and they have intermittently been subjected to severe criticism. Yet a blended or compromise statistics, mainly Fisherian, soon emerged in a range of practical and scientific fields, from agriculture and ecology to psychology, therapeutic medicine, and the social sciences. These versions of statistics, which vary somewhat from field to field, have mostly been treated within their disciplines as gospel.
Spiegelhalter criticizes Fisher’s statistics on a number of counts. We would not ordinarily expect an otherwise genial textbook-like introduction to a field to be so critical of prevailing practices. But statistics has long been riven by intense controversy. Although the disagreements persist, they have of late become less virulent. Still, Spiegelhalter and many of his colleagues remain critical of the statistical practices of various scientific fields. Perhaps the worst offenses are associated with pharmaceutical testing and social psychology, both of which have come in for harsh criticism. Statisticians are not alone in perceiving some very serious problems. Some of those problems, Spiegelhalter suggests, reflect fundamental shortcomings of Fisher-style statistics. In particular, Fisher’s canonical p-values (.05 and .01) do not give us what we want, the probability that a cause is real; rather, they give us something more difficult to interpret, the probability that we would have a deviation of this magnitude without such a cause. Other problems may be understood as abuses to which these methods are vulnerable in the hands of researchers who have a stake in the outcome of the analysis.
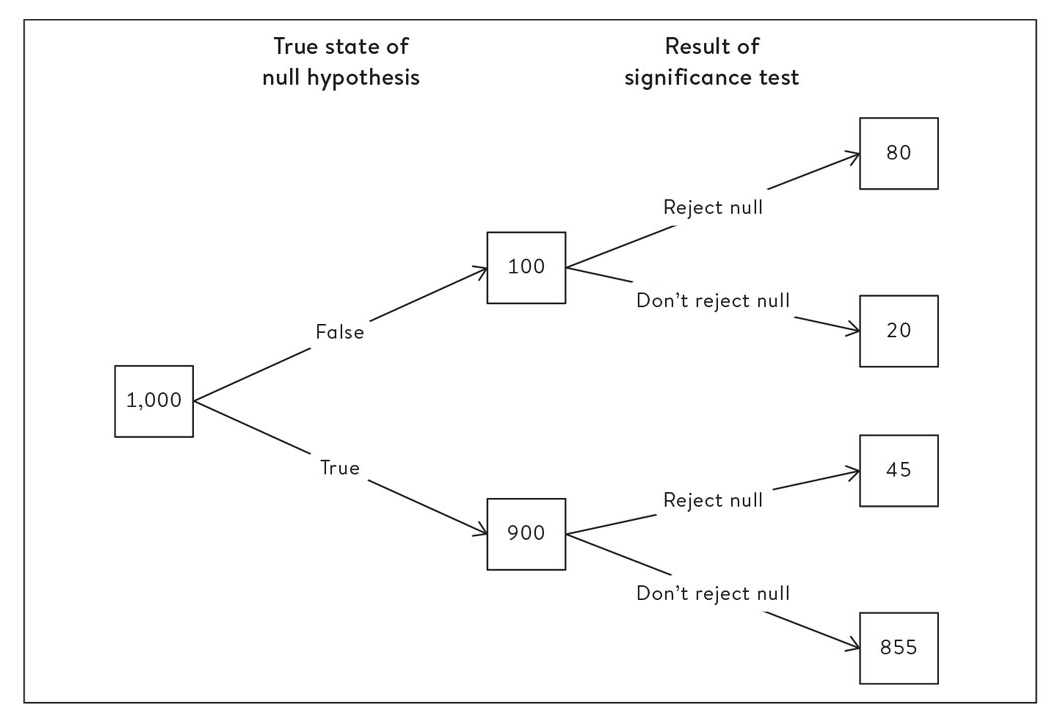
From The Art of Statistics.
Although The Art of Statistics is written for an intelligent popular audience rather than for professional statisticians, it provides hints and examples of what the author sees as a better approach to statistics. He is less insistent on controlled experimentation, and more sympathetic to methods that take into account our prior expectations, than are many scientists. He devotes a whole chapter to a defense of Bayesian methods, which indeed are endorsed by many statisticians.
Bayesians hold that statistical analysis should incorporate the reasonable beliefs (priors) that we bring to a question. They are willing to pay the price of relying on numbers that may appear to be arbitrary or ungrounded. One extreme example, attributed to John Maynard Keynes, envisages a game of poker with the Archbishop of Canterbury, who in the first hand deals himself a straight flush (Spiegelhalter has “royal flush,” but that doesn’t accord with the odds he gives and doesn’t match other published versions of the anecdote). Did the archbishop cheat? Bayesian probability offers a way to redeem his reputation. The probability of a being dealt a straight flush in a fair game is only 1 in 72,000, making such a deal highly unlikely to happen by chance. But before the poker game began, Spiegelhalter argues, we might have reasonably thought that the archbishop would be extremely unlikely to cheat; we might even have reckoned his prior probability of dishonesty to be as low as 1 in 1,000,000. Comparing that very low, wholly subjective figure to the 1 in 72,000 figure may make us feel more inclined to attribute the straight flush to chance rather than to cheating. In this fashion, a subjective impression of probability can overwhelm an otherwise compelling calculated probability.
Can a postulated probability like the one in this example, which seems so arbitrary, really have a role in sober science? Perhaps. I can imagine, in a discussion among friends, trying out different probability values as a means of groping toward a shared opinion. But such discussion is far removed from the sort of reasoning that has made statistics so central to science, bureaucracy, and medicine. It has mainly been worked out and routinized as the basis for decisions with serious consequences, such as drug licensing, or as a criterion of impersonal science. In those circumstances, invented numbers don’t cut it. In pharmaceutical trials, billions of dollars are often at stake. The Archbishop of Canterbury might be able to maintain his disinterestedness in the face of such temptations (who can say?), but profit-driven corporations, on the evidence, are not able to do so. The temptations do not disappear with the redefinition of statistics as the algorithmic analysis of big data.
Sometimes, however, the shortcomings of statistics are attributable to incapacity rather than deceit. Weighty medical decisions regarding painful or dangerous treatments are often based on calculations involving, for example, base rates, false positives, and false negatives—numbers that most people, even very intelligent ones, find it difficult to apply correctly. One key ambition of The Art of Statistics is to put forward representations of data that any educated person can understand and deploy appropriately. It is heartening to find that expert statisticians and psychologists are willing to invest time and energy in such efforts.
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.