The Thermodynamic Sinks of this World
By Roald Hoffmann
What would an elemental soup cook up to?
What would an elemental soup cook up to?

DOI: 10.1511/2013.103.260
Supposing you have a stew of all the elements, in sufficient quantity, a good way to mix them, a temperature intermittently high enough to get all molecules and extended solids to fall apart to atoms or ions, lots of time—what would you have in the end, when such a world cooled to a specified temperature?
This is a Gedankenexperiment. I am ignoring here the astrophysical history of the universe. No world where my experiment might be relevant exists—each star, planet, satellite, asteroid has had a history. And that history has certainly involved nonequilibrium conditions, whereas I am trying to impose equilibrium. Am I after a chimera then, something completely irrelevant to this world? I don’t think so—the minerals of Mars are by and large the same minerals as those of our moon or the Earth, and the atmosphere of Titan contains no molecules strange to Earth, be they present in very different ratios. What, then, are the most stable compounds of this world, of any world?
That those gleaming brass 19th-century steam engines of the Midlands could not deliver energy at more than about 10 percent efficiency was not understandable until heat and work and energy and entropy were precisely defined. So it is with stability. There are three sorts of what is colloquially called “energy”—energy (E), enthalpy (H = E + PV), and what used to be called Gibbs free energy and now is termed Gibbs energy (G = E + PV – TS), where P, V and T are pressure, temperature and volume, respectively, and S is the entropy. (Skipped here are some fine points of which thermodynamic variables are kept constant.)
The Gibbs energy change (ΔG) in a reaction determines the position of the equilibrium in a reaction
A + B ↔ C + D,
that is, whether there is a lot of reactant A + B, or product, C + D. If ΔG is negative, product dominates; if ΔG is positive, reactant is present in greater amount. We also need the words exothermic and endothermic—these refer to heat changes and can be related to negative ΔH (exothermic, heat released in a reaction as written, left to right) or positive ΔH (endothermic, heat absorbed in a reaction). At low temperatures, as T > 0 kelvin, exothermic reactions go to the right, endothermic ones to the left.
Time for an example or two. Here are two possible equilibria in my model world, at room temperature:
Na (s) + ½ Cl2 (g) ↔ NaCl (s) ΔH = –411 kJ/mol
H2 (g) + ½ O2 (g) ↔ H2O (l) ΔH = –286 kJ/mol
The units of the enthalpy here and throughout this essay are kilojoules per mole (kJ/mol), and s, l and g stand for solid, liquid and gas, respectively. The source of the heats is the wonderfully useful (yet not infallible) NIST Chemistry WebBook, NIST Standard Reference Database Number 69, http://webbook.nist.gov/chemistry/. They are all rounded off to 1 kJ.
I have not chosen these reactions for nothing; they are examples of general salt (not just sodium chloride) and oxide formation, two of the avenues to great stability that we will encounter. Both reactions are highly exothermic. The second is a lecture demonstrator’s standby, the hydrogen balloon. As you have seen, nothing much happens … until a flame or a spark is brought up. Then the reaction goes, with a satisfying bang. For the sodium-chlorine reaction, to get it going one needs to melt the sodium, or put a drop of water on it.
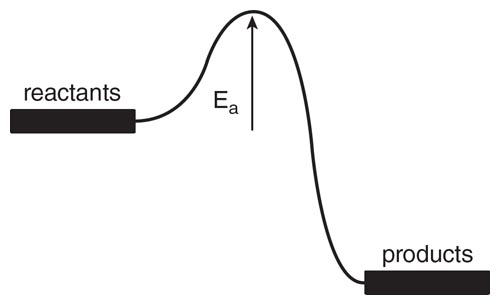
Illustration by Tom Dunne
For both reactions there is an activation energy, Ea, larger for the water formation. A schematic diagram of what is happening, energy-wise, in the course of the reaction is shown in the figure above. Here is the reason for specifying high temperatures in my Gedankenexperiment—I want to be able to overcome all barriers and just wind up with the most stable materials.
Going back to the cartoon world of H2, Cl2, O2 and Na, you would get mostly NaCl (s) and H2O (l) at equilibrium at 298 kelvin. Not really—for mixing is most certainly allowed, and salt dissolves spontaneously in water, as you well know. And perhaps I should worry about other reactions among the six species. For instance Na with H2 (to give NaH [s]), Na with O2 (to give Na2O [s]), Cl2 with H2 (to give HCl [g]), Cl2 with O2 (to give Cl2O or ClO2, both known). And I haven’t started to be concerned about ternaries (compounds of three elements with each other); I’ve kept my world simple with binaries, isolated from each other. Remember that other pyrotechnic lecture demonstration—dropping a chunk of sodium into water?
Na (s) + H2O (l) ↔ NaOH (aq) + ½ H2 (g) ΔH = –183 kJ/mol
I write NaOH (aq), the “aq” standing for aqueous, because NaOH is very soluble in water (ΔG for solution is –42 kJ/mol). Now how about quaternaries?
If the temperature is very high, the entropy term in ΔG will steer things, so that reactions in which the entropy is increased are favored. All solids will be spontaneously converted into gases. Yes, even solid NaCl (boiling point [b.p.] = 1,413 degrees Celsius) and NaOH (b.p. 1,388 degrees Celsius). All molecular gases will decompose into atoms, a reaction with a nice positive ΔS, as translational degrees of freedom are created. And some ions will be created (for example, H ↔ H+ + e-), depending on the temperature. From a chemist’s point of view, the surface or interior of a star (now that is high T!) is boring—there are no molecules there. But from a nuclear physicist’s point of view, these are the greatest fun.
The low temperature limit, T approaching absolute zero, poses different problems. For then the history of the model world really, really matters. Let me explain. At very low temperatures, the atoms are not moving quickly enough to overcome in their collisions any barriers (remember the ubiquitous activation energies introduced above?). So if you take that hydrogen balloon with its mixture of H2 and O2 down to close to absolute zero, you will have to wait a very, very long time, a time approaching infinity, to get any water. Here H2 and O2 are metastable relative to H2O, perfectly happy on their own. You can see what I mean by history—at low T what you get (in a human, finite observation time) depends on whether the reactant molecules were first heated to overcome activation barriers. Or if they were not, just allowed to cool.
The high vacuum interstellar medium poses another challenge. If a rare collision between two molecules or atoms that are prone to react were to take place—say H2 + O (atomic)—the reaction to H2O being highly exothermic (by 491 kJ/mol, gas phase) the product molecule is born with a large energy. In the absence of collisions, that energy will have nowhere to go, and the reaction, exothermic, will not happen.

Image courtesy of NASA/JPL—Caltech/Cornell/Arizona State Unvierstiy.
The surfaces of dust grains and cooled planetary objects present a special environment: high vacuum on one side, but an inert, or potentially catalytic, solid surface on the other. Low temperatures (unless there is volcanic activity)—but a long, long time. And sporadic influx of energy in the form of light. This is a wonderfully interesting set of conditions, important for the evolution of complex chemistry or life. But it isn’t quite my model world.
I built my world as one of essentially limitless amounts of each element. If instead I began with equal and large finite masses, I would immediately run into the constraints of a limiting reagent. Consider for instance that simple water-forming reaction. If you have a finite amount (say 16 grams each) of H2
and O2, you will get at equilibrium 18 grams of H2O, with 14 grams of H2
left over and a miniscule amount of O2. Thirty-two grams we began with, 32 grams we have at the end—from Lavoisier’s time we knew that nothing is gained, nothing is lost. And let’s not worry about what mass/energy equivalence leads to in an exothermic reaction. There just wasn’t enough O2
there to react with the H2
supplied.
Here’s the nagging thought then about the utility of my Gedankenexperiment — any real world must begin with pretty constrained if not fixed local concentrations of the elements. And so the outcome of all reactions, not just for the equal-mass example above, will be constrained by those initial conditions. We will come back to this.
Let’s use some simple chemistry to get a feeling for the thermodynamic sinks of this world. We are looking for compounds with the most negative heats of formation. A heat of formation is defined as the enthalpy change (under standard terrestrial conditions, P = 1 atmosphere, T = 298 kelvin) for the process
A + B + C ↔ AB n Cm,
where A, B and C are the elements and ABnCm a compound. Here it is a ternary, but the generalization is obvious.
Let’s start with carbon and oxygen. The well-known oxides of carbon are CO, CO2, and carbon suboxide, C3O2 . Other oxides, CnO2, n = 2–7; CnO, n > 2; and CnOn, n = 2–6, are also experimentally known in small amounts, trapped in an inert matrix at low temperatures. The heats of formation of the oxides available in quantity are –110 (CO, [g]), –394 (CO2, [g]), –122 (C3O2, [l]) kJ/mol, respectively. Note the negative heats of formation, indicating stability with respect to the elements. Here is the first principle of stability, one we have already seen in the reaction forming water: Form oxides. This is confirmed for every element, except the noble gases. And gold. Incidentally, quartz, SiO2, is “better” than CO2, for the heat of formation of the former is a whopping –911 kJ/mol.
One oxide of carbon, CO2, is much more stable than the others. This can be checked by calculating from the above heats of formation the energetics of all possible interconversion reactions, for example, CO2 ↔ CO + ½ O2, 3CO2 ↔ C3O2 + 2O2 and so forth, and finding them all positive, endothermic.
But … if one introduced a lot of Ca in the environment, the Ca would react with CO2 (enough heat supplied to overcome all barriers) to give CaCO3, calcium carbonate, limestone, a real thermodynamic sink:
Ca (s) + ½ O2 (g) + CO2 (g) ↔ CaCO3 (s) ΔH = –813 kJ/mol
Is this going to go on? That is, are we going to get in a mix of 100 or so elements (let’s not worry about the late actinides) a most stable compound of “multinary” composition, AxByCzDw…? I don’t think so. Metastable molecules with more than 10 elements are known, and solid state compounds of 9 elements at least. But I think both experience and intuition indicate that such multielement compounds are likely to be unstable with respect to disproportionation or reaction with oxygen.
So what are the real thermodynamic sinks of this world? The place to look is with simple compounds with highly negative heats of formation. We have already met four such: NaCl, H2O, CO2, CaCO3. Their heats of formation are –411, –286, –394, –1,207 kJ/mol. The prescription is obvious: Form oxides, form solid state, ionic compounds. The elements don’t stand a chance, except for the early noble gases (the heats of formation of the xenon fluorides are not large, but negative).

Image courtesy of NASA GSFC.
Following up the clue from the low heat of formation of calcite, one finds that all carbonates are very stable, as are most salts containing nitrate (NO3-), sulfate (SO42-), phosphate (PO43-) and silicate ions. For instance the heat of formation of calcium phosphate (Ca3(PO4)2) is –4,132 kJ/mol, that of Fe2(SO4)3 –2,583 kJ/mol. After a while one realizes that what matters is the heat of formation increment per atom, so these values become somewhat less spectacular than they seem. But they are large and negative, for sure.
The stuff of this Earth, minerals such as silicates, also have very highly negative heats of formation. Their presence in planetary bodies, including ours, is evidence to their stability. Much more needs to be said about the silicates, which constitute up to 90 percent of the Earth’s crust. These occur in a remarkable variety, with cations of every kind coordinating to [SiO4]4- (olivine, for example), [Si2O7]6- (epidote), [SinO3n]2n- (tourmaline), [Si4nO11n ]6n- (hornblende), [Si2nO5n]2n- (clays and mica), [AlxSiyO2(x+y)]x- (zeolites; x = 0, y = 1 is quartz). Along this series, the degree of cross-linking or O-coordination increases. Thus olivine has isolated SiO4 tetrahedra, whereas the various forms of quartz feature an interlinked three-dimensional network of the same. This is the Bowen reaction series, and as one progresses along it, one gets silicates that crystallize at lower temperatures from a magma—are more stable.
There is a pattern emerging in the nature of the more stable compounds: It’s not simply ionic bonding (Na+Cl-, Li+H-), but ionic bonding between an alkali or alkaline earth cation and a molecular anion (CO32-, SiO44-). Of course, within each molecular ion there lurks ionicity—the bonds that connect the centering N or C or Si or S atoms to oxygen in these anions are polar. Ions within ions!
But there are compounds more stable than oxides, and these are fluorides—for example, CaF2, fluorite, or Na3AlF3, cryolite. In these even more ionicity is provided than in oxides. The thermodynamic stability of all ionic fluorides, the magnitude of their negative heats of formation per atom, is astonishingly high. This can be understood in a qualitative way: The energy required to break apart the element, F2 molecules, is small. The electron affinity the resulting F atoms is as large as they get. And the size of the F- anion is relatively small, so that one gets a lot of electrostatic stabilization in inorganic fluoride crystals (the so-called Madelung energy).
Also, in the temperature range where water is a liquid, a good number of salts, hardly all, dissolve in water with a negative Gibbs energy of solution. The entropy contribution to this Gibbs energy change is often large, if not dominant, for obvious reasons. I don’t think other polar solvent liquids (each with their own temperature range of stability), such as ammonia, SO2, HF or supercritical CO2, will provide as much stabilization as water does.
So my tentative answer to the question posed at the beginning is not romantic. The final product (at P = 1 atmosphere and 298 kelvin) will be a messy soup of cations of the less electronegative elements (including the transition metals) with molecular anions, in water. Some pretty insoluble salts of similar composition (minerals!) will be there. And the first few noble gases standing by, if they are not allowed to escape.
When I first posed the question of the thermodynamic equilibrium at a research group meeting, I thought I’d find a ready analysis in any geochemistry text. I found some (see, for instance, the last section in Konrad Krauskopf’s older Introduction to Geochemistry), but not much. The reason is that my question is a theorist’s dream, and geochemists are practical people. Here is what J. Donald Rimstidt of Virginia Tech told me:
The phase or substance that is stable at a given temperature and pressure is not just controlled by its free energy of formation, but it is affected by the bulk composition of the system. As a result, geochemists are concerned with elemental abundances and the physical processes that affect abundances. Once the elemental abundances for a region have been established, then we draw a box around that region and use equilibrium thermodynamics to predict the phase or species distribution. This local equilibrium assumption works well for some cases (especially at high temperature and pressure). At earth-surface conditions, where chemical reaction rates as well as mass transport rates can be slow, metastable conditions can persist regardless of the scale of the model domain.
His last point, the persistence of metastable molecules and minerals, is one I made above. More important, geochemists don’t worry about my castle-in-the-sky equilibrium world, because … the Earth (and every object in the universe) has a history. There is no infinitely replenishing cornucopia of all elements; even if we chose our region as big as the universe, the abundance of the elements is constrained by the physics of nucleosynthesis in the moments after the Big Bang, and in the subsequent more drawn out formation of heavier elements in stars and supernovae.
Remember those fluorides, the most stable of compounds? Why isn’t the world full of fluorides? Because the abundance of the element fluorine in the universe, in the Solar System, and in the Earth is relatively small.
A beautiful account of the evolution of minerals has been given by Robert M. Hazen, of the Carnegie Institution, and his coworkers. To quote the abstract of their paper:
The stages of mineral evolution arise from three primary mechanisms: (1) the progressive separation and concentration of the elements from their original relatively uniform distribution in the pre-solar nebula; (2) an increase in range of intensive variables such as pressure, temperature, and the activities of H2O, CO2, and O2; and (3) the generation of far-from-equilibrium conditions by living systems.
The first stage led to the approximately 250 minerals found in unweathered meteorite samples, the second to about 1,500 other minerals, and the third, directly or indirectly, to most of the Earth’s 4,200 known mineral species.
I’ve set up the equilibrium world, the one thermodynamics seems to say we should have. As interesting as it is, we don’t have it, and no exoplanet will have it either. The building blocks are present in constrained amounts. Radioactive decay and large mass combine to build up temperatures and drive plate tectonics, processes that in turn lead to quite specific mineral forming events. For a given size planet, in time all the lighter noble gases will escape, as they by and large did here. If the size of the planet, volcanic activity, sources of energy are not right, water will disappear too or freeze, and dissolution of salts will not take place.
Then there is life. James Lovelock’s Gaia hypothesis, bolstered by Lynn Margulis’s insight, is that life creates disequilibrium. The abundant oxygen in our atmosphere (when there are so many ways to fix it, as we have seen) is direct testimony to the planet-forming power of life. There are theories of maximum entropy flow driving systems inevitably off equilibrium. Yet these theories are contested.
I think history—physical law + variety + happenstance, call it hazard, in the old, original sense of the word—creates and propagates a state off equilibrium, even without life. And there is no way to turn off history. We have a chanced, beautiful planet, its surface and atmosphere way off the thermodynamic state I’ve tried to explore. We had better be careful of what we have.
I am grateful to useful comments setting me straight by Mainak Mookherjee, Vaclav Smil, Don Rimstidt, Tyler Volk, David Schwartzman, Eugen Schwarz, Andreas Hermann and Michael O’Keeffe.
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.