Pencil, Paper, and Pi
By Brian Hayes
A gargantuan calculation of pi in the 1850s ran up against the limits of manual arithmetic; figuring out where it went wrong calls for forensic mathematics.
A gargantuan calculation of pi in the 1850s ran up against the limits of manual arithmetic; figuring out where it went wrong calls for forensic mathematics.

DOI: 10.1511/2014.110.342
William Shanks was one of the finest computers of the Victorian era—when the term computer denoted not a machine but a person skilled in arithmetic. His specialty was mathematical constants, and his most ambitious project was a record-setting computation of pi. Starting in 1850 and returning to the task at intervals over more than 20 years, he eventually published a value of pi that began with the familiar digits 3.14159 and went on for 707 decimal places.
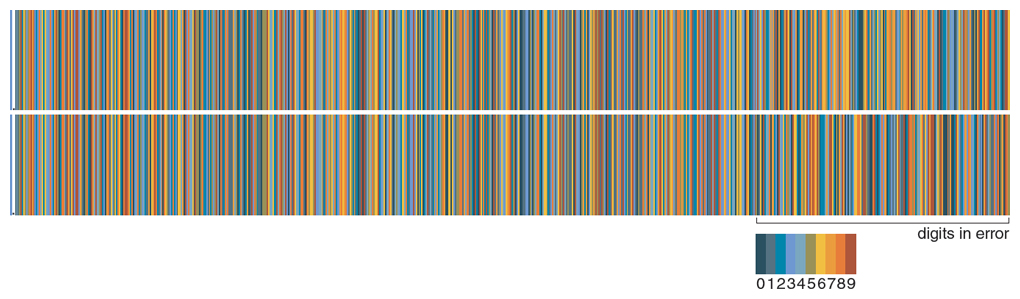
Illustration by Brian Hayes.
Seen from a 21st-century perspective, Shanks is a poignant figure. All his patient toil has been reduced to triviality. Anyone with a laptop can compute hundreds of digits of pi in microseconds. Moreover, the laptop will give the correct digits. Shanks made a series of mistakes beginning around decimal place 530 that spoiled the rest of his work.
I have long been curious about Shanks and his 707 digits. Who was this prodigious human computer? What led him to undertake his quixotic adventures in arithmetic? How did he deal with the logistical challenges of the pi computation: the teetering columns of figures, the grueling bouts of multiplication and division? And what went wrong in the late stages of the work?
One way to answer these questions would be to buy several reams of paper, sharpen a dozen pencils, and try to retrace Shanks’s steps. I haven’t the stamina for that—or even the life expectancy. But by adapting some pencil-driven algorithms to run on silicon computers, I have gotten a glimpse of what the process might have been like for Shanks. I think I also know where a couple of his errors crept in, but there are more that remain unexplained.
Biographical details about William Shanks are hard to come by. It’s known that he was born in 1812, married in 1846, and died in 1882. He came from Corsenside, a village in the northeast of England, near the Scottish border. After his marriage he lived in Houghton-le-Spring, another small northeastern town, where he ran a boarding school.
Some sources identify Shanks as a student of William Rutherford, a mathematician who taught at the Royal Military Academy and also dabbled in pi calculations. It’s true that Shanks studied with Rutherford, but this was not the relationship of a graduate student with a thesis advisor. When Shanks published a small book on pi in 1853, he dedicated it to Rutherford, “from whom I received my earliest lessons in numbers.” It turns out that Rutherford taught at a school not far from Corsenside in the 1820s. Shanks was then a boy of 10 or 12, and he must have been one of Rutherford’s pupils.
I have not been able to learn anything about Shanks’s further education; there is no mention of a university degree. Rutherford remained a mentor and became a collaborator. The two men cross-checked their calculations of pi and published some of the results jointly.
The available evidence suggests that Shanks was an amateur and a marginal figure in the mathematical community, but not a crank. He published 15 papers in the Proceedings of the Royal Society. Although he was never a member, he apparently had no trouble persuading Fellows to submit manuscripts on his behalf. These sponsors—some of whom were also listed as subscribers to his 1853 book—included prominent figures in British science and mathematics: George Stokes, George B. Airy, William Whewell, Augustus De Morgan.
Pencil-and-paper computation was a skill more highly prized in the 19th century than it is today. Even then, however, grinding out 707 decimal places of pi was more of a stunt than a contribution to mathematical research. Shanks seems to have understood the borderline status of his project. The book he wrote about his calculations begins:
Towards the close of the year 1850, the Author first formed the design of rectifying the Circle to upwards of 300 places of decimals. He was fully aware, at that time, that the accomplishment of his purpose would add little or nothing to his fame as a Mathematician, though it might as a Computer; nor would it be productive of anything in the shape of pecuniary recompense at all adequate to the labour of such lengthy computations. He was anxious to fill up scanty intervals of leisure with the achievement of something original, and which, at the same time, should not subject him either to great tension of thought, or to consult books.
He was surely right about the limited payoff in fame and funds. I hope he managed to avoid tension of thought.
There are countless ways of computing pi, but almost all 19th-century calculators chose arctangent formulas. These methods begin with a geometric observation about a circle with radius 1 and circumference 2pi. As shown in the diagram below, an angle drawn at the center of the circle defines both an arc along the circumference and a right triangle with sides a, b, and c. The arctangent function relates the length of side b (the “side opposite” the angle) to the length of the arc. In particular, when b has length 1, the arc is one-eighth of the circumference, which is equal to pi/4. The equation arctan 1 = pi/4 is the key to computing pi. If you can assign a numerical value to arctan 1, you get an approximation to pi/4; multiply this number by 4 to get a value for pi itself.
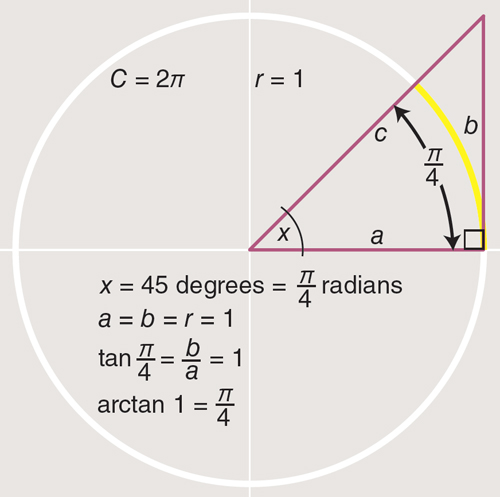
Illustration by Brian Hayes.
The next question is how to compute an arctangent. The pioneers of calculus devised an infinite series that gives the value of arctan x for any value of x between –1 and +1:
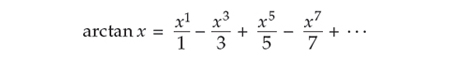
For the case of x = 1, the series assumes a particularly simple form:
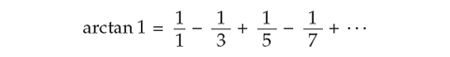
Hence to calculate pi one can just add up the terms of this series—the reciprocals of successive odd numbers, with alternating plus and minus signs—until the sum attains the desired accuracy.
Lamentably, this plan won’t work. At x=1 the arctan series converges at an agonizingly slow pace. To get n digits of pi, you need to sum roughly 10n terms of the series. Shanks would have had to evaluate more than 10700 terms, which is beyond the means of even the most intrepid Victorian scribbler.
All is not lost. For values of x closer to zero, the arctan series converges more quickly. The trick, then, is to combine multiple arctan calculations that sum up to the same value as arctan 1. Shanks worked with the following formula, discovered in 1706 by the English mathematician John Machin:
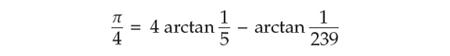
He had to evaluate two arctan series rather than just one, but both of these series converge much faster.
The illustration below traces the evaluation of the first three terms of the series for arctan 1/5 and arctan 1/239, retaining five decimal places of precision. The error in the computed value of pi is 0.00007. No extraordinary skill in arithmetic is needed to carry out this computation by hand. But now imagine scaling it up to several hundred terms and several hundred decimal places. The basic operations remain the same, but keeping all the figures straight becomes a clerical nightmare.

Illustration by Brian Hayes.
In computing arctan 1/5, Shanks evaluated 506 terms, each carried to 709 decimal places. Most likely he performed separate summations of the positive and negative terms. If he tried to write down such an addition problem all in one piece—253 rows of 709-digit numbers, or almost 180,000 digits in all—it would fill a sheet of paper two meters wide by a meter high. Breaking the task down into smaller pieces makes it less awkward physically but entails other costs: extra copying of intermediate results, transferring carry digits, the risk of misaligning columns or rows.
Erwin Engert, a Shanks enthusiast, has tested the travails of pencil-and-paper calculation by doing 20-digit and 40-digit evaluations of Machin’s arctan formula. The results are on his website at http://engert.us/erwin/Miscellaneous.html. The challenge of keeping digits aligned became severe enough that Engert printed ruled forms for the larger computation. Shanks may well have done the same, although we have no direct evidence.
In silico, summing n terms of the series for arctanx takes just a few lines of code:

For each integer k from 0 to n–1, the program generates an odd integer m and the corresponding term of the arctan series, xm/m. The expression (–1)k sets the sign of the term—plus for even k, minus for odd. When the loop completes, the function returns the accumulated sum of the n terms. The only hidden subtlety here is that the numeric variables must be able to accommodate numbers of arbitrary size and precision.
No one doing arithmetic with a pencil would adopt an algorithm anything like this one. After every pass through the loop, the program throws away all its work except the variables k and sum, then starts from scratch to build the next term of the series. A manual worker would surely save the value of xm as a starting point for calculating the next power, xm+2. And exponentiating –1 is not how a human computer would keep track of alternating signs.
It’s not hard to transform the program into a more pencil-friendly procedure, avoiding needless recomputation and saving intermediate results for future use. Moreover, the computer can be programmed to use digit-by-digit algorithms—the ones we all learned in elementary school, and forgot soon after—for multiplication and long division. But these alterations still fail to capture some important practices of a shrewd human reckoner.
Most of the terms in the series for arctan 1/5 are repeating decimals with a short period. For example, the term (1/5)9/9 works out to 0.000000056888…. A naive computer program would go on dividing digit after digit out to the limit of precision, but Shanks surely just filled in a string of 8s.
There are also peculiarities of base 10 to be taken into account. For generating the sequence of odd powers of 1/5, the basic step is dividing by 25. Engert suggests dividing by 100 (a shift of the decimal point) and multiplying by 4. Another option is to calculate (1/5)m as 2 m/10m (where again division by a power of 10 is just a decimal-point shift). I mention this latter possibility because Shanks’s book on the pi computation includes a table of the powers of 2 up to 2721. Did he use those numbers to compute his powers of 1/5, or were they just for checking values computed in some other way?
Shanks doesn’t reveal much about his computational methods, and I remain unsure about several aspects of his strategy. For example, a term in the series for arctan 1/5 can be written either as (1/5)m/m or as 1/(m5m). Mathematically these expressions are identical, but they imply different computations. In the first case you multiply and divide long decimal fractions; in the second you build a large integer and then take its reciprocal. Which way did Shanks do it? He doesn’t say. If I were to attempt to replicate his work, I might stick with decimal fractions for arctan 1/5, because of the many short-period repetitions, but I might choose the reciprocal method for arctan 1/239, because taking a reciprocal is a little easier than other forms of division.
As Tolstoy might have said, all correct computations are alike, but every erroneous one errs in its own way. In that spirit, the incorrect digits in Shanks’s result are much more informative than the correct ones. If nothing else, they might reveal just where and how his computation went off the rails.
Shanks published his value of pi in three stages. A January 1853 article (under Rutherford’s byline) includes 530 decimal places; 440 of those figures were confirmed by Rutherford, and the rest were also correct apart from a few typographical errors and a discrepancy in the last two digits that could be attributed to round-off.
In the spring of 1853, Shanks extended his calculation from 530 to 607 decimal places, publishing these results in a privately printed book, Contributions to Mathematics, Comprising Chiefly the Rectification of the Circle to 607 Places of Decimals. This is where the errors creep in. His value of arctan 1/5 goes awry in the 530th decimal place, right on the boundary between the old and the new computations. Because arctan 1/5 is multiplied by 16 in the Machin formula, the error propagates back to the 528th decimal place in the value of pi. Shanks’s sum for arctan 1/239 is also incorrect, starting at the 592nd decimal place.
After bringing out his book, Shanks put pi aside for 20 years. When he took up the task again in 1873, he extended the two arctan series to 709 decimal places and pi to 707. Because these computations were built atop the flawed earlier work, they were doomed from the start. The errors weren’t noticed until 75 years later, when D. F. Ferguson, working with a mechanical desk calculator, extended a new calculation of pi beyond 700 digits.

Illustration by Brian Hayes.
Trying to discover where Shanks went wrong is an interesting exercise in forensic mathematics. Usually, one strives to find the correct answer to a problem; here the aim is to get the wrong answer—but the right wrong answer. We want to take a correct value and find some way of modifying it that will yield the specific erroneous output reported by Shanks. It’s like searching for a suspicious transaction when your checkbook disagrees with the bank statement, except that we have no access to the individual checkbook entries, only the final balance.
To search for an error in the arctan 1/5 series, I took the difference between the true value and Shanks’s value, then subtracted this discrepancy from each of the 506 terms of the series. In most cases the result was uninformative, but my eye was drawn to this pattern, in the 248th term:
T: 7444668008 0 48 3 89738430583501
S: 7444668008483897384305835010
Sequence T comes from the true arctan sum, starting at decimal place 520; sequence S is the same region after subtracting the discrepancy. In the first 10 positions the two numbers agree, but thereafter S is a shifted version of T, created by omitting the 0 marked in red and letting the rest of the digits slide left one place. (There’s also a substitution a few digits later, where a 2 becomes a 3.)
Without further documentary evidence, it’s not possible to prove that this spot marks the site of Shanks’s first error, but it’s certainly a plausible hypothesis. When Shanks extended this term from 530 digits to 609, he didn’t need to do any actual arithmetic. The term is a repeating decimal with a period of 210 digits, so he merely needed to copy a segment from earlier in the sequence. It seems likely that he missed that 0 digit while copying. I was not the first to discover this error; Erwin Engert identified it before I did.
If you inject this one-digit shift error into the arctan calculation, the output matches the Shanks value in the region following decimal place 530, but the agreement does not continue all the way to the end. At decimal place 569 the two sequences part ways again. Evidently there’s another mistake.
I wasn’t the first to notice this problem, either. In 1946 Ferguson called attention to an anomaly in term 72 and suggested that Shanks had omitted all the digits of this term from position 569 on. I believe that Ferguson correctly identified the trouble spot, but his diagnosis is not quite right. Truncating term 72 in this way does not transform the correct sum into the Shanks value. But another simple change does work: omitting five digits at position 569 and shifting the rest of the term to the left.
With these two “uncorrections,” we can transform the true value of arctan 1/5 into the Shanks value through decimal place 601. At that point there must be yet another error, but the situation is confusing. The last eight digits of the 609-place value published in 1853 differ from the corresponding digits listed in 1873. I have not found a simple error that yields either version. The error in arctan 1/239 also remains unexplained.
It’s curious that Shanks produced almost 530 flawless digits of pi, then made at least four mistakes in the next 80 digits. All four errors date from March or April of 1853, and they seem to be clerical rather than mathematical. I can only speculate on the cause of this sudden spate of carelessness. Perhaps Shanks was hurrying to get his book into the hands of the subscribers. Or maybe, at age 41, he was experiencing the early symptoms of presbyopia.
Stories about Shanks tend to focus on the mistakes. We look back with pity and horror on all those pages of meticulous arithmetic rendered worthless by a slip of the pencil. But I would argue that even with the errors, Shanks’s computation of pi was an impressive endeavor. His 527 correct digits were not bettered for almost a century. Augustus De Morgan, one of the leading mathematicians of the era, had his doubts about Shanks’s work, but he also spoke admiringly of “the power to calculate, and… the courage to face the labour.”
For further material on Shanks, including references and programs for exploring his computation, see http://bit-player.org/shanks.
©Brian Hayes
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.