American Scientist

IN PURSUIT OF THE TRAVELING SALESMAN: Mathematics at the Limits of Computation. William J. Cook. xiii + 228 pp. Princeton University Press, 2012. $27.95.

Back in the early 1950s, three mathematicians at the RAND Corporation, the Santa Monica think tank, took on the notorious traveling salesman problem, or TSP. The imaginary peddler in this problem has clients in a number of cities and wants to plan the shortest possible tour that visits each city and then returns to the starting point. The RAND group—George Dantzig, Ray Fulkerson and Selmer Johnson—set to work on a specific instance of the problem, searching for the shortest circuit through 49 U.S. cities. They selected one city in each of 48 states, plus Washington, D.C., and looked up the distances between pairs of cities in a road atlas.

A direct approach to the salesman’s problem is easy to describe and understand: Just list every possible ordering of the cities and choose the sequence that yields the lowest total mileage. This algorithm is guaranteed to work, although not necessarily in the lifetime of the solar system. Suppose you start the tour in Washington. You have 48 candidates for your first destination city; then, no matter which of the 48 you choose, there remain 47 unvisited cities to consider for the third slot in the tour, and so on. The number of permutations is 48 × 47 × 46 × . . . × 1, which works out to about 10⁶¹, far beyond the realm of practicality even for the fastest of modern computers. Yet Dantzig, Fulkerson and Johnson solved the 49-city problem with more modest machinery: pencil and paper, augmented with pegs and string. They placed the pegs on a wooden map, then stretched the string around pegs in various configurations to measure and compare routes. At the end of their labors they found a loop with a total length of 12,345 miles. What’s more, they proved that no other circuit passing through all the cities can yield a shorter tour.

In spite of this spectacular early success, the TSP has become famous mainly for its difficulty. If you need an algorithm that always identifies the optimal tour, then nothing substantially better than the exhaustive enumeration of all possible routes has ever been discovered. Indeed, the TSP belongs to a family of problems that share the same stigma of intractability. In the classification of computing problems as “P” or “NP”—labels that correspond, roughly, to “easy” and “hard,” respectively—the TSP is a standard-bearer for the NP class. If you found an efficient algorithm for the TSP, it could be adapted to solve all the other NP problems as well; but the smart money in computer science bets that no such algorithm exists. Thus from the point of view of computing theory, all NP problems are pretty much alike, and they’re all hopeless.

This is not the attitude of William J. Cook, whose book In Pursuit of the Traveling Saleman celebrates all the idiosyncrasies of this particular problem and emphasizes how much progress has been made in solving instances of practical interest, despite the gloomy theoretical outlook. He is personally responsible for a big chunk of that progress. Cook and three of his colleagues are the creators of Concorde, a computer program that has broken many records for TSP solutions, including one example that laces an optimal path through 85,900 sites.

How can a problem be certifiably hard but also solvable in practice? The formal categories of P and NP impose a severe standard: An algorithm proposed as a solution to a problem must work correctly on every instance and must always produce the best possible answer. Life is not quite so grim if you relax these requirements just a little. It turns out there are many TSP algorithms that succeed most of the time but occasionally fail, or whose answers are good but not always best. The central chapters of Cook’s Pursuit describe the art and craft of getting the most out of such incomplete and approximate methods.

Consider that a shortest tour of the United States is unlikely to begin by zigzagging across the continent, say, from Washington to Phoenix, back to Boston and then westward again to Seattle. An optimal tour is more likely to chain together nearby cities—Washington and Baltimore, Seattle and Portland. This commonsense observation is the basis of several heuristic algorithms, such as a “greedy” method that starts by linking nearest neighbors. For one important class of problems (those where the distances or travel costs between cities obey the “triangle inequality,” a + b ≥ c), some of the heuristic methods are guaranteed to find a route that is no more than twice the optimum.

Another strategy is to produce a pretty-good tour and then search for ways to improve it. The simplest such transformation is a 2-opt move, in which two links of the tour are removed, leaving in temporary isolation four cities that can be reconnected in a different sequence to yield a smaller total distance. For example, the zigzag Washington-Phoenix-Boston-Seattle route is easily improved by making such a 2-opt exchange.

The most fruitful idea of all comes from a very different branch of mathematics: the optimization technique known as linear programming. The classic applications of linear programming are tasks such as finding the most profitable mix of products for an oil refinery. The TSP is also an optimization problem, but adapting it to the linear programming infrastructure required considerable ingenuity. The reward is that linear programming not only helps find good tours but can also establish lower bounds. That is, a linear programming algorithm can prove that no circuit through a given set of cities can possibly have a length less than x miles; if you then find an x-mile tour, you know it is optimal.

All of these tricks and many others are exploited by the Concorde TSP software. Cook has released a version of this program as a free “app” for the iPhone and the iPad (see http://www.tsp.gatech.edu/iphone/index.html). It solves the Danzig-Fulkerson-Johnson problem in two seconds.

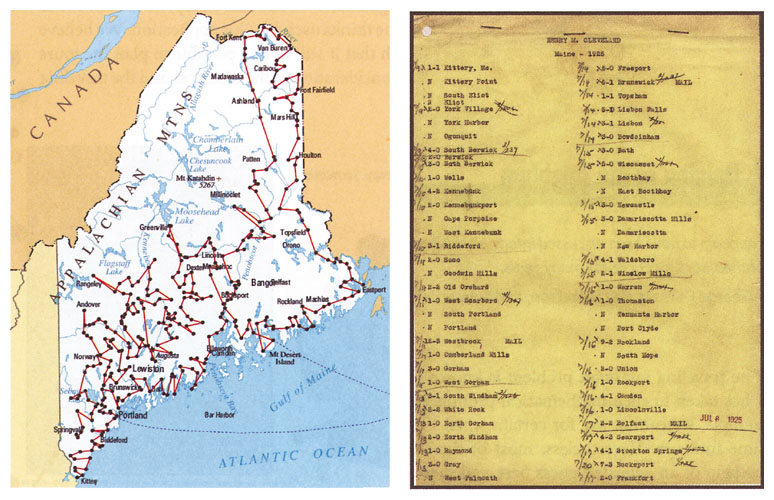
Along with a heady dose of algorithms, Cook also offers a diverting survey of the lore and history of the TSP. The most charming revelation is that the problem’s name is more than fanciful: Real traveling salesmen have struggled over their itineraries, without the aid of higher mathematics and computing machinery. Cook cites a 1925 exchange of letters between the home office of the Page Seed Company and Henry M. Cleveland, a salesman covering the New England states. That summer Cleveland made stops in some 350 places in Maine, and he was none too happy with the route suggested by the office.

Dear Sirs
My route list is balled up the worst I ever saw. Will take half as long again to work it as last year. . . . The river from Bangor down has no bridge and you have those towns down as if I could cross it anywhere. Last year’s list was made out the best of any one and I can’t see the object of changing it over. I think I have made myself plain.

In Pursuit of the Traveling Salesman is in some respects a condensed edition of an earlier book, The Traveling Salesman Problem: A Computational Study, by Cook and three more coauthors: David L. Applegate, Robert E. Bixby and Vašek Chvátal. The new volume addresses a wider audience, with more pictures and fewer equations, explaining how things are done rather than how to do them, but it covers all the same territory as the larger book. The path through that territory seems reasonably close to optimal.