
This Article From Issue
May-June 2003
Volume 91, Number 3
DOI: 10.1511/2003.44.0
Hinged Dissections: Swinging and Twisting. Greg N. Frederickson. xii + 287 pp. Cambridge University Press, 2002. $45.
Students of mathematics often find themselves identifying with one of two distinct camps within the subject: algebraists and geometers. At the risk of a bit of caricature, I would say that the algebraists tend to play with symbols and the geometers with pictures. Greg Frederickson's Hinged Dissections is emphatically a book for the geometers. It's an extended meditation on the fun of playing with pictures. It may even convince a few algebraists to come over to the other side.
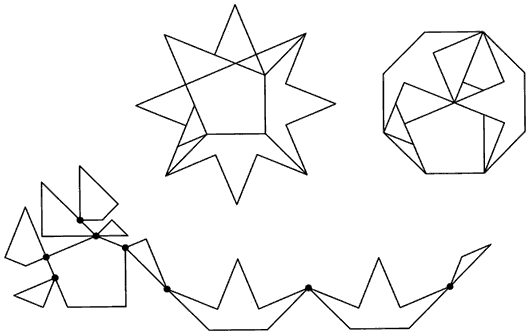
From Hinged Dissections.
The book focuses on a special class of dissection problems, those in which the goal is to slice up shape A into pieces that can then be rearranged to form shape B. Such problems have an ancient pedigree (dating back at least to Plato), and Frederickson has already authored the indispensable book on the subject of dissection problems in general—Dissections: Plane and Fancy (Cambridge University Press, 1997). In this newer book, the dissection problems come with a restriction: Not only must we slice up shape A and rearrange it into shape B, but we must do so in a way that makes use of hinges linking the various slices together. For the greater part of the book, Frederickson employs "swing hinges" that restrict particular vertices of the distinct pieces to be identified in both shapes A and B and that also disallow "twisting" pieces out of the plane. Many of the examples in the book dissect one large shape into smaller ones by using separate "chunks" of hinged pieces, but the most jaw-dropping examples are those in which a single collection of hinged pieces can be rearranged into two remarkably different forms.
In a succession of increasingly startling chapters, Frederickson describes hinged dissections created both by himself and by others. Since dissection fans paid little attention to "hingeability" until a few years ago, most of the examples are recent; in some cases, "classic" dissections also happen to be hingeable. (Frederickson shows two simple but lovely dissections of this sort created by Leonardo da Vinci.) Like a magician pulling a succession of stranger and wilder animals out of his hat, the author shows dissections from multiple polygons (squares, triangles, hexagons, octagons) to one; dissections involving crosses (Maltese, Latin, Greek); and dissections involving curved forms, stars and (in an extended aside) polyominoes. In the final chapters of the book, we encounter three-dimensional hinged dissections (one beautiful but very straightforward example rearranges two truncated octahedra into a cube), and two-dimensional dissections with more powerful hinges that allow pieces to "flip around" out of the plane, either around a vertex (flip hinges) or around the midpoint of an edge (twist hinges). The book is truly a feast, not so much for the eye as for the "inner eye": The real fun is in staring at the diagrams and imagining the transition between shape A and shape B via the "spread out" hinged forms that Frederickson depicts. The diagrams are clear and (as far as this reader can discern) accurate and beautifully edited.
I have a few quibbles. Like many books in recreational mathematics, Frederickson's is much stronger at presenting the fruits of the creators' labors (the solutions to the various dissection problems) than the nature of creation itself. How does one come up with a reasonable dissection problem, and how does one go about seeking a solution? The book describes several general techniques for creating hingeable dissections (the most powerful such technique involves superposing planar tessellations that contain the two target shapes), but many of Frederickson's examples clearly require specific techniques and tricks beyond the obvious. Here, the descriptions are rather telegraphic. (And how to create or visualize three-dimensional dissections is left almost a complete mystery.) I would have loved to see some photographs of actual models of hinged dissections. The book does give some helpful hints on how to create these models out of wood or cardboard, and these must make for absolutely killer demonstrations in any geometry class. Finally, the book employs a leitmotif in which the description of a geometric puzzle by turn-of-the-century British puzzle writer Henry Dudeney is progressively deconstructed (textually, not geometrically!); this turns out to be less fun than the biographical asides that Frederickson employed in his earlier book.
But these are very mild quibbles indeed. I would put Frederickson's dissection books, along with Alan Holden's Shapes, Space, and Symmetry (Columbia University Press, 1971), on the shortlist of beautiful, inspirational and accessible works in recreational geometry. I heartily recommend Hinged Dissections to anyone who loves geometry, or wants to.
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.