American Scientist

Flocks of starlings, herds of zebra, schools of mackerel, traffic jams, a nuclear chain reaction, an ant colony, fairy rings of fungi, the spinning electrons of a ferromagnet, a forest fire spreading from tree to tree, the spiral arms of a galaxy, epidemic disease. What golden thread ties together the items on this motley list? They are all phenomena that emerge from the interactions of many individual things. Multiplicity is essential here: One zebra does not make a herd, nor one car a traffic jam. But there is unity too: The herd, the traffic jam, the magnet and the galaxy have an existence of their own, with properties different from those of their constituents. After all, a flock can't flap its wings, and a bird can't split itself in two to fly around an obstacle.

Computer simulation offers an attractive way to explore these curious, one-from-many systems. A simulation can be built from the bottom up, starting with the rules that govern the individual actors—birds, stars, cars, ants and so on. If these "microscopic" laws are correct, the "macroscopic" behavior of the higher-level system should emerge automatically, just as it does in nature. You don't have to teach a herd of zebra how to stay together; you only have to tell the individual zebras how to get along with their nearest neighbors.

A programming system called StarLogo is designed for building simulations of just this kind. StarLogo is the creation of Mitchel Resnick of the Epistemology and Learning Group in the Media Laboratory at the Massachusetts Institute of Technology. Resnick describes the system and explains the ideas behind it in his 1994 book Turtles, Termites and Traffic Jams: Explorations in Massively Parallel Microworlds. StarLogo software is freely distributed over the Internet; for more information see the note at the end of this article.

PG-13

StarLogo is an offspring of Logo, the programming language devised in the 1960s by Seymour Papert of MIT and Wallace Feurzeig of Bolt, Baranek and Newman. The best-known feature of Logo is turtle graphics, a scheme for drawing pictures by issuing commands to a "turtle" that carries a pen over a plane. The first turtles, which actually predated Logo by two decades, were mechanical devices that crawled on the floor or a tabletop. Today most Logo systems provide a "virtual turtle" on a computer display screen.

StarLogo extends the turtle-graphics metaphor in three ways. First, it accommodates thousands of turtles rather than just one or a few. Second, the turtles can interact with one another and with their environment; for example, one turtle might deposit a chemical, which would then be sensed by other turtles. Third, the environment itself becomes more than a passive background for the simulation. The landscape where the turtles live and move is made up of "patches," which can be assigned various properties. In effect, the turtles wander over a two-dimensional cellular automaton, which would be a powerful computing device even without the turtles.

Here is the Logo idiom for drawing a circle:

to logo-circle
pendown
repeat 360 [forward 1 left 1]
end

The turtle repeatedly moves one step forward and turns one degree left until it comes back to its starting point. The same procedure would work without alteration in StarLogo, but other approaches to circle drawing make better use of StarLogo's distinctive facilities. The emphasis in StarLogo is less on pens and drawing and more on creating patterns with the turtles themselves. Here is one way to create a circle in StarLogo:

to starlogo-circle
create-turtles 2000
setheading random 360
forward 40
end

The idea is to spawn a large number of turtles, all initially at the origin of the plane, and then send them marching 40 steps in random directions. The result is a ring of turtles with a radius of 40 units.

The first version of StarLogo was written for the Connection Machine, the fine-grained parallel computer created by Danny Hillis. The Connection Machine was particularly well suited to the task because its thousands of processors allowed each turtle to run its own independent program. But not everyone has a Connection Machine in the basement. Current versions of StarLogo run on the Macintosh computer, where parallel execution has to be simulated on a single processor. Even so, programs with several thousand turtles run with acceptable speed.

Papert developed Logo as "a language for learning," and in particular as a language that would help to acquaint children with the enchantments of computer programming. Resnick also has an interest in pedagogical matters, but he suggests the ideal audience for StarLogo is somewhat older than that for Logo Classic: He gives the language a PG-13 rating. Many interesting StarLogo programs have been written by high school students, and I have found that even adults can pick up the basic principles with only a little effort.

How to Think Like a Slime Mold

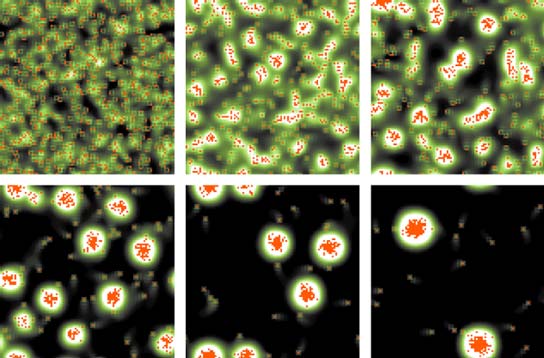
The archetype of all StarLogo simulations is a model of cellular slime molds, such as Dictyostelium discoideum, creatures balanced on the borderline between protozoa and multicellular organisms. For most of its life, a slime mold is a single-celled amoeba, grazing in the soil or leaf litter for bacteria. But when food runs short, the slime mold undergoes a remarkable transformation. Thousands of cells stream toward gathering points, where they clump together to form a roving animal called a slug (though it is unrelated to the molluscan slugs); then the cells differentiate further into a more plantlike stalk structure, which finally emits spores that disperse and produce a new generation of amoebas.

It is the aggregation stage in this life cycle that lends itself to study by StarLogo simulation. The slime molds are summoned to the family reunion by a chemical cue, which in Dictyostelium is cyclic adenosine monophosphate (cAMP). An early hypothesis was that a few "founder" cells secrete the cAMP, becoming beacons for the assembly of the slug. But later experiments showed that all the cells secrete cAMP. It took some time to understand how the cells could assemble without leaders to rally around, but a StarLogo model readily reproduces the behavior.

In the model, the amoeboid cells are represented by turtles, which secrete cAMP into the underlying patches. The cAMP then diffuses into neighboring patches, and it also gradually loses its potency over time. The cells' movements are governed by a gradient-following rule: Each cell examines its immediate surroundings and generally moves toward the neighboring patch that has the highest concentration of cAMP, although there is a little randomness in the motion.

That's all there is to the model. The program includes no mechanism to decide where the cells will congregate, and there are no designated leaders or founders; all of the cells obey exactly the same rules. Nevertheless, cells scattered at random over the landscape soon clump together in colonies of 50 or 100. If the simulation is allowed to continue, some of these groups eventually coalesce into still larger aggregations. After many thousands of time steps, most of the amoebas are inside a few large and stable clusters.

Watching the model in action, it's easy to understand what's happening. Each cell exudes a halo of cAMP, which diffuses through the underlying patches and attracts other cells that happen to pass nearby. If two or three cells are close together, their pooled secretions produce a stronger chemical signal, which tends to hold the cells together and also attracts more passersby. Positive feedback keeps the process going: The more cells gather in a region, the more cAMP accumulates there to attract other cells.

Of course a model this simple can't capture all the details of slime-mold biology. For example, real slime-mold amoebas gather in waves or pulses, which have no counterpart in the simulation. But the computer model has an advantage when it comes to exploring hypothetical changes in the cells' behavior. Consider the gradient-following algorithm, which the program deliberately makes imperfect by adding a random "wiggle" to the cells' direction-finding procedure. A biological experiment to study this effect would be difficult to engineer, but in the computer model it's a matter of changing a couple of numbers. Adding more wiggle breaks up the clusters, which is not surprising since randomly wandering cells cannot respond reliably to a cAMP gradient. But what happens when you eliminate the randomness? I thought I knew the answer. I thought the random noise was needed to break out of local optima, and that without it the cells would get stuck in small clusters that never grew into big ones. The actual result is more interesting. With perfect gradient following you see not only stationary, disk-shaped clumps but also long trains of cells that march across the landscape as coherently moving clusters, maintaining their identity even when they collide and pass through one another. I'm not sure what to make of this observation. When I mentioned it to Resnick, he responded that it might possibly reveal something about the biology of slime molds, but it could also very well be an artifact of the StarLogo system.

Boids of a Feather

Bird flocks are another classic application of StarLogo modeling. Starlings and several other bird species assemble in large cluster flocks that perform synchronized, balletic flights, wheeling and swooping over autumn fields. People have long wondered both why and how they do it. For a time the "how" question was considered a problem in animal communication: How can the birds signal their intentions quickly enough to coordinate the group's sudden movements? There was even a suggestion (by Edmund Selous, in a bizarre but charming book published in 1931) that flocking birds must rely on some form of "thought transference" or "collective thinking" for synchronization. It was only in the 1980s that another kind of explanation came into favor. That new idea was inspired in part by computer simulations.

In discussing the history of ideas about bird flocks, Frank Heppner of the University of Rhode Island has written that "a zeitgeist was at large" in the mid-1980s, when several workers independently devised similar theories. Heppner himself was one of the theorists; he "suggested that flocking might be an emergent property arising out of simple rules of movement followed by individuals in the flock." At about the same time Craig W. Reynolds, then at Symbolics Inc., produced a computer simulation of flocking "boids" that relied entirely on local interactions between near neighbors. (The boids attracted attention not only among biologists and computer scientists but also in Hollywood; Reynolds recently received an Academy Award for his work on this and several other animations.)

Reynolds's boids obeyed three main rules: 1) Avoid collisions. 2) Try to match the speed and direction of nearby boids. 3) Move toward the "center of gravity," or the mean position, of the nearby boids. An even simpler flock simulation is included among the sample programs shipped with the StarLogo software. At each time step, each bird finds its nearest neighbor among all its flockmates. (If there are multiple nearest neighbors, all at the same distance, one is chosen arbitrarily.) If the chosen neighbor is closer than a predetermined threshold distance, the bird flies in the opposite direction; if the neighbor is farther than the threshold, the bird flies toward it; if the distance is just right, the bird matches the neighbor's heading. Thus each bird interacts with only one neighbor at a time. This rudimentary model will not win any Oscars, but it creates flocks that do seem recognizably avian.

Stop and Logo

Traffic jams are a particularly intriguing topic for StarLogo models because we experience them from the inside. We may never know exactly what motivates an amoeba or a bird, but we have a very good idea of how a driver thinks and acts on the freeway at rush hour.

Resnick tells the story of writing a traffic simulation with some high school students. They programmed the cars to obey a follow-the-leader rule: If you're too close to the car in front, slow down; otherwise accelerate to the speed limit and maintain that speed. The students also created a roadside radar trap, where cars would momentarily brake; they predicted that this disturbance would cause a traffic jam. The prediction was correct. But then the students removed the radar trap and were surprised to find that traffic still bogged down, without any apparent cause.

Highway engineers are certainly familiar with this phenomenon—and so are drivers. You toil slowly through a mile of bumper-to-bumper traffic, expecting to find an accident or repair work obstructing the roadway, but when you get to the head of the queue, there's nothing to be seen. The congestion develops and dissipates spontaneously. Macroscopic explanations of this effect often invoke analogies with fluid dynamics or with the theory of phase transitions and critical phenomena. For example, a spontaneous jam might be compared with a shock wave propagating backward through the moving stream of traffic.

The StarLogo simulation offers a more intimate, driver's eye view of what goes on inside a traffic jam. The two rules that drivers obey are enough on their own, without any external trigger, to make the flow of traffic unstable. If a random fluctuation in speed or position brings you close to the car ahead, the rules require you to slow down. Thereafter the car behind you may also have to slow, and the car behind that one too. On the far side of the congested segment, cars leave the jam one by one. When it is your turn, you suddenly find the road ahead clear, and you can accelerate to maximum speed again. Indeed, the jam has the interesting effect of regulating the spacing of cars on the downstream side, so that traffic flows more smoothly than it would have without the jam. In the little world of StarLogo, however, the highway is actually a loop, and cars that exit at the right edge re-enter at the left; hence the traffic jam you've just escaped is one you will soon encounter again.

Apartheid

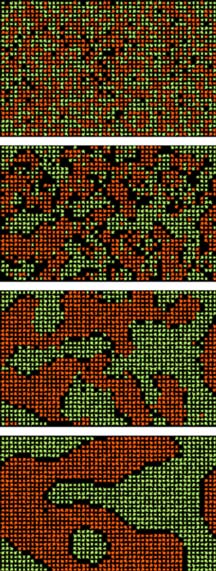
The StarLogo model I have found most provocative is one that Resnick presents as a fable about frogs and turtles living together in a pond. Initially the two species occupy lily pads in a checkerboard pattern, so that each animal's eight neighbors include an equal number of frogs and turtles. Then one night a storm overturns all the lily pads, and in the morning the animals find themselves randomly rearranged. Frogs and turtles are tolerant of each other, but neither wants to be entirely isolated from their own species. So the unhappy frogs—those that happen to have too few frog neighbors—abandon their lily pads and choose a new home at random. The unhappy turtles do the same. After this migration, there may still be unhappy animals, and so the procedure is repeated until all find an acceptable neighborhood.

The social implications of this model are easier to see than the zoological ones. And the most interesting observation to come out of it is that even a moderate preference for living among your own kind can give rise to a dramatic pattern of segregation. What starts out as a salt-and-pepper mixture gradually evolves, over a few hundred iterations, into large blobs of almost uniform composition. Even though none of the individuals insist on racial purity, most of them wind up living with a very high percentage of neighbors like themselves.

It's an intriguing result, but as I watched the model evolving, with the frogs and turtles slowly withdrawing into their own territories, I began to have misgivings. In the first place, the patterns looked suspiciously familiar. I had seen them before in models that depict the onset of magnetization in ferromagnets and the separation of oil and water. What these latter processes have in common is that they tend to minimize surface area (or the area of interface between phases). It's not implausible that racial segregation also shares this tendency, and the discovery of a connection between a social process and certain physical systems would be illuminating. On the other hand, seeing the frogs-and-turtles model in that context turns it into a more generic bit of mathematics. The gears and levers of the underlying differential equations are showing through.

The model has some other curious features as well. As the desired fraction of like neighbors increases from 30 to 60 percent, the pattern of segregation grows more extreme, as one might expect. But what happens in a population of more radical segregationists, who won't be content unless at least 80 percent of their neighbors are of their own kind? Paradoxically, the system remains thoroughly integrated. Except at low population density, the proportion of like neighbors seldom departs far from 50 percent. The reason, of course, is that everybody is unhappy. Very few of the participants ever achieve their 80-percent target, and so most of the population is randomly rearranged on every trial. I think this is an unlikely outcome in a city of bigots.

Mindsets

StarLogo is one of the most beautiful computer toys I've ever encountered. It is ingenious in concept and brilliantly executed. Writing StarLogo programs is a delight. The language offers high leverage: A few lines of code can yield deep results. The implementations work smoothly and reliably. There's an active community of StarLogo enthusiasts. The sample projects distributed with the software cover an amazing range of topics.

But StarLogo is not a Model of Everything. One limitation is that it's strictly two-dimensional. These turtles crawl; they don't swim or dive. The programmer also has no choice about the geometry or the boundary conditions of the StarLogo world. On the screen it is a square or rectangular place; topologically it is a torus, where right meets left and up meets down.

Another constraint on StarLogo models is the emphasis on local interactions. StarLogo lends itself most naturally to situations where signals pass between nearest neighbors, as in the slime mold model. In effect, the turtles have acute senses of touch and smell, but their hearing and vision are weak. Long-range interactions and global knowledge are hard to fit into StarLogo programs. This may partly explain the breakdown of the race-relations model. In a real city, residents know more about racial distribution than just the identity of their immediate neighbors, and someone seeking a homogeneous environment would not have to choose a new home at random.

Of course Resnick makes no claim that StarLogo is the universal key to understanding the world, but he does suggest some analogies and connections that may not stand up to scrutiny. In his book and other writings he speaks of the "decentralized mindset." Centralized leadership and control are being replaced by self-organizing structures and systems, he argues. He cites among his examples the collapse of centrally planned economies in Eastern Europe and the triumph of free-market capitalism. He also mentions a shift in corporate organization away from a hierarchical chain of command toward decentralized management, and the trend in computing to replace central computers with distributed processing. It's easy to see a resemblance between these developments and the kinds of models constructed with StarLogo, but I'm not convinced the connection runs very deep. In particular, economic activity is not constrained to local interactions, which makes StarLogo models of markets and businesses seem rather artificial. On the other hand, a weakness of some other simulation systems is that they totally ignore spatial factors, so perhaps this is a needed correction. In any event, StarLogo is a magnificent tool for thinking about decentralized systems.

Getting StarLogo

Download the StarLogo system system from MIT. At Tufts University the Connected Mathematics project (led by Uri Wilensky) has created an extended language called StarLogoT, which only runs on the Macintosh. A Java version is in preparation.

© Brian Hayes