Computational Thinking in Science
By Peter J. Denning
The computer revolution has profoundly affected how we think about science, experimentation, and research.
The computer revolution has profoundly affected how we think about science, experimentation, and research.

DOI: 10.1511/2017.124.13
A quiet but profound revolution has been taking place throughout science. The computing revolution has transformed science by enabling all sorts of new discoveries through information technology.
Throughout most of the history of science and technology, there have been two types of characters. One is the experimenter, who gathers data to reveal when a hypothesis works and when it does not. The other is the theoretician, who designs mathematical models to explain what is already known and uses the models to make predictions about what is not known. The two types interact with one another because hypotheses may come from models, and what is known comes from previous models and data. The experimenter and the theoretician were active in the sciences well before computers came on the scene.

When governments began to commission projects to build electronic computers in the 1940s, scientists began discussing how they would use these machines. Nearly everybody had something to gain. Experimenters looked to computers for data analysis—sifting through large data sets for statistical patterns. Theoreticians looked to them for calculating the equations of mathematical models. Many such models were formulated as differential equations, which considered changes in functions over infinitesimal intervals. Consider for example the generic function f over time (abbreviated f(t)). Suppose that the differences in f(t) over time give another equation, abbreviated g(t). We write this relation as df(t)/dt=g(t). You could then calculate the approximate values of f(t) in a series of small changes in time steps, abbreviated Δt, with the difference equation f(t+Δt)≈f(t)+Δtg(t). This calculation could easily be extended to multiple space dimensions with difference equations that combine values on neighboring nodes of a grid. In his collected works, John von Neumann, the polymath who helped design the first stored program computers, described algorithms for solving systems of differential equations on discrete grids.
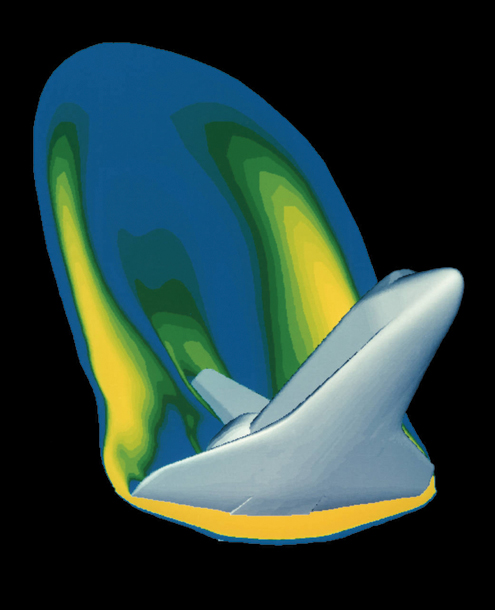
Image courtesy of NASA.
Using the computer to accelerate the traditional work of experimenters and theoreticians was a revolution of its own. But something more happened. Scientists who used computers found themselves routinely designing new ways to advance science. Simulation is a prime example. By simulating airflows around a wing with a type of equation (called Navier-Stokes) that is broken out over a grid surrounding a simulated aircraft, aeronautical engineers largely eliminated the need for wind tunnels and test flights. Astronomers similarly simulated the collisions of galaxies, and chemists simulated the deterioration of space probe heat shields on entering an atmosphere. Simulation allowed scientists to reach where theory and experiment could not. It became a new way of doing science. Scientists became computational designers as well as experimenters and theoreticians.
Scientists who used computers found themselves routinely designing new ways to advance science. They became computational designers as well as experimenters and theoreticians.
Another important example of how computers have changed how science is done has been the new paradigm of treating a physical process as an information process, which allows more to be learned about the physical process by studying the information process. Biologists have made significant advances with this technique, notably with sequencing and editing genes. Data analysts also have found that deep learning models enable them to make surprisingly accurate predictions of processes in many fields. For the quantities predicted, the real process behaves as an information process.
The two approaches are often combined, such as when the information process provides a simulation for the physical process it models.
The term computational science, and its associated term computational thinking, came into wide use during the 1980s. In 1982, theoretical physicist Kenneth Wilson received a Nobel Prize in physics for developing computational models that produced startling new discoveries about phase changes in materials. He designed computational methods to evaluate the equations of renormalization groups, and used them to observe how a material changes phase, such as the direction of the magnetic force in a ferrimagnet (in which adjacent ions have opposite but unequal charges). He launched a campaign to win recognition and respect for computational science. He argued that all scientific disciplines had very tough problems—“grand challenges”—that would yield to massive computation. He and other visionaries used the term computational science for the emerging branches of science that used computation as their primary method. They saw computation as a new paradigm of science, complementing the traditional paradigms of theory and experiment. Some of them used the term computational thinking for the thought processes in doing computational science—designing, testing, and using computational models. They launched a political movement to secure funding for computational science research, culminating in the High-Performance Communication and Computing (HPCC) Act passed in 1991 by the U.S. Congress.
Computational thinking emerged from within scientific fields—it was not imported from computer science. Indeed, computer scientists were slow to join the movement.
It is interesting that computational science and computational thinking in science emerged from within the scientific fields—they were not imported from computer science. Indeed, computer scientists were slow to join the movement. From the beginnings of computer science in the 1940s, there was a small but important branch of the field that specialized in numerical methods and mathematical software. These computer scientists have the greatest affinity for computational science and were the first to embrace it.
Computation has proved so productive for advancement of science and engineering that virtually every field of science and engineering has developed a computational branch. In many fields, the computational branch has grown to constitute the majority of the field. For example, in 2001 David Baltimore, Nobel laureate in biology, said that biology is an information science. Most recent advances in biology have involved DNA modeling, sequencing, and editing. We can expect this trend to continue, with computation invading deeper into every field, including social sciences and the humanities. Many people will learn to be computational designers and thinkers.
Computational thinking is generally defined as the mental skills that facilitate the design of automated processes. Although this term traces back to the beginnings of computer science in the 1950s, it became popular after 2006 when educators undertook the task of helping all children become productive users of computation as part of STEM education. If we can learn what constitutes computational thinking as a mental skill, we may be able to draw more young people to science and accelerate our own abilities to advance science. The interest from educators is forcing us to be precise in determining just what computational thinking is.
Most published definitions to date can be paraphrased as follows: “Computational thinking is the thought processes involved in formulating problems so that their solutions are represented as computational steps and algorithms that can be effectively carried out by an information-processing agent.” This definition, however, is fraught with problematic ideas. Consider the word “formulating.” People regularly formulate requests to have machines do things for them without having to understand how the computation works or how it is designed. The term “information agent” is also problematic—it quickly opens the door to the false belief that step-by-step procedures followed by human beings are necessarily algorithms. Many people follow “step-by-step” procedures that cannot be reduced to an algorithm and automated by a machine. These fuzzy definitions have made it difficult for educators to know what they are supposed to teach and how to assess whether students have learned it.
And what “thought processes” are involved? The published definitions say they include making digital representations, sequencing, choosing alternatives, iterating loops, running parallel tasks, abstracting, decomposing, testing, debugging, and reusing. But this is hardly a complete description. To be a useful contributor, a programmer also needs to understand enough of a scientific field to be able to express problems and solution methods appropriate for the field. For example, I once witnessed that a team of computational fluid dynamics scientists invited PhD computer scientists to work with them, only to discover that the computer scientists did not understand enough fluid dynamics to be useful. They were not able to think in terms of computational fluid dynamics. The other team members wound up treating the computer scientists like programmers rather than peers, much to their chagrin. It seems that the thought processes of computational thinking should include those of skilled practitioners of the field where the computation will be used.
All these difficulties suggest that the word “thinking” is not what we are really interested in—we want the ability to design computations. Design includes the dimensions of listening to the community of users, testing prototypes to see how users react, and making technology offers that take care of user concerns. Therefore computational design is a more accurate term. It is clearly a skill set, not a body of mental knowledge about programming.
An essential aspect of computational design (or thinking) is a machine that will carry out the automated steps. But most computational designers do not directly consider the hardware of the machine itself; instead they work with a computational model, which is an abstract machine—basically a layer of software on top of the hardware that translates a program into instructions for the hardware. Designers are not concerned with mapping the model to the real machine, because that’s a simulation job that software engineers take care of.
In computing science, the model most talked about is the Turing machine, which was invented in 1936 by computing pioneer Alan Turing. His model consists of an infinite tape and a finite state control unit that moves one square at a time back and forth on the tape, reading and changing symbols. Turing machines are the most general model for computation—anything that people reasonably think can be computed, can be computed by a Turing machine.
But Turing machines are too primitive to easily represent everyday computation. With each new programming language, computer scientists defined an associated abstract machine that represented the entity programmed by the language. Software called a compiler then translated the language operations on the abstract machine into machine code on the real hardware.
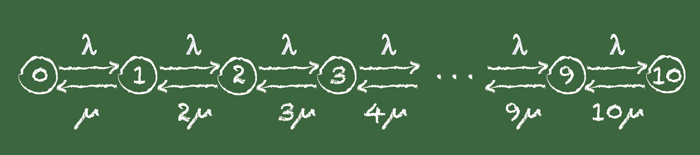
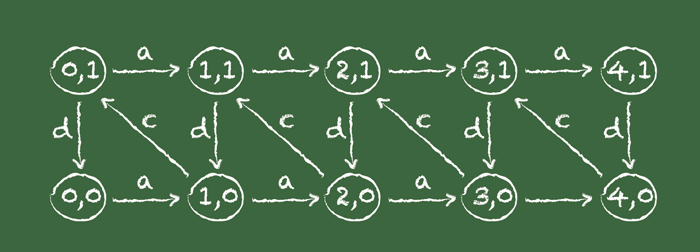
The models of the Turing machine and of programming languages are all general purpose—they deal with anything that can be computed. But we often work with much less powerful models that are still incredibly useful. One of the most common is the finite state machine, which consists of a logic circuit, a set of flip-flop switch circuits to record the current state, and a clock whose ticks trigger state transitions. Finite state machines model many electronic controllers and operating system command interpreters.
The typical artificial neural network is an even simpler model. It is a loop-free network of gates modeled after neurons. The gates are arranged in layers from those connected to inputs to those connected to outputs. A pattern of bits at the input passes through the network and produces an output. There is no state to be recorded or remembered. Each signal from one layer to the next has an associated weight. The network is trained by an algorithm that iteratively adjusts the weights until the network becomes very good at generating the desired output. Some people call this machine learning because the trained (weight-adjusted) circuit acquires a capability to implement a function by being shown many examples. It is also called deep learning because of the hidden layers and weights in the circuit. Many modern advances in artificial intelligence and data analytics have been achieved by these circuits. Simulations of these circuits now allow for millions of nodes and dozens of layers.
When you go outside computer science, you will find few people talking about Turing machines and finite state machines. They talk instead of machine learning and simulation of computational models relevant to their fields. In each field, the computational designer either programs a model or designs a new model—or both.
There are many problems that cannot be solved at all with computation; their solutions will emerge only from social cooperation among groups.
An important issue with computational models is complexity—how long does it take to get a result? How much storage is needed? Very often a computational model that will give you the exact answer is impossible, too expensive, or too slow. Computational designers get around this with heuristics—fast approximations that generate close-approximation solutions quickly. Experimental validation is often the only way to gain trust in a heuristic. An artificial neural network for face recognition is a heuristic. No one knows of an exact algorithm for recognizing faces. But we know how to build a fast neural network that can get it right most of the time.
Computing has changed dramatically since the time when computational modeling grew up. In the 1980s, the hosting system for grand-challenge models was a supercomputer. Today the hosting system is the entire Internet, now more commonly called the cloud—a massively distributed system of data and processing resources around the world. Commercial cloud services allow you to mobilize the storage and processing power you need when you need it. In addition, we are no longer constrained to deal with finite computations—those that start, compute, deliver their output, and stop. Instead we now tap endless flows of data and processing power as needed and we count on the whole thing to keep operating indefinitely. With so much cheap, massive computing power, more people can be computational designers and tackle grand challenge problems.
But there are important limits to what we can do with all this computing power. One limit is that most of our computational methods have a sharp focus—they are very good at the particular task for which they were designed, but not for seemingly similar tasks. We can often overcome that limit with a new design that closes a gap in the old design. Facial recognition is an example. A decade ago, we did not have good methods of detecting and recognizing faces in images—we had to examine the images ourselves. Today, with deep learning algorithms, we have designed very reliable automated face recognizers, overcoming the earlier gap.
Another limit is that there are many problems that cannot be solved at all with computation. Some of these are purely technical, such as determining by inspection when a computer program will halt or enter an infinite loop. Many others are very complex issues featuring technologies intertwined with social communities and no obvious answers—which are known as wicked problems. Many wicked problems are caused by the combined effects of billions of people using a technology. For example, the production of more than a billion refrigerators releases enough fluorocarbons to disrupt the upper atmosphere’s protection against excessive sunlight. Millions of cars produce so much smog that some cities are unhealthy. The only solutions to these problems will emerge from social cooperation among the groups that now offer competing and conflicting approaches. Although computing technology can help by visualizing the large-scale effects of our individual actions, only social action will solve the problems we are causing.
Still, computational science is a powerful force within science. It emphasizes the “computational way” of doing science and turns its practitioners into skilled computational designers (and thinkers) in their fields of science. Computational designers spend much of their time inventing, programming, and validating computational models, which are abstract machines that solve problems or answer questions. Computational designers need to be computational thinkers as well as practitioners in their own fields. Computational design will be an important source of work in the future.
Click "American Scientist" to access home page
American Scientist Comments and Discussion
To discuss our articles or comment on them, please share them and tag American Scientist on social media platforms. Here are links to our profiles on Twitter, Facebook, and LinkedIn.
If we re-share your post, we will moderate comments/discussion following our comments policy.